— DEV — Energy levels of an “artificial atom” - Spherical and ellipsoidal CdSe Quantum Dot

Attention

This tutorial is under construction

Input files:

• QDArtificialAtom_CdSe_3D_spherical_nnp.in

• QDArtificialAtom_CdSe_3D_ellipsoidal_nnp.in

• ParabolicQW_GaAs_2D_nnp.in

Scope:

• In this tutorial we calculate the eigenenergies of a spherical and ellipsoidal CdSe quantum dot (“artificial atom”). The tutorial is based on [Ferreira2006].

Output files:

• bias00000\Quantum\energy_spectrum_quantum_region_Gamma_00000.dat

• bias00000\Quantum\interband_matrix_elements_quantum_region_HH_Gamma.txt

Energy levels of an “artificial atom” - Spherical CdSe Quantum Dot

Here, we want to calculate the energy levels and the wave functions of a spherical CdSe quantum dot of radius \(r = 5~\mathrm{nm}\) shown in Figure 2.4.225.

Figure 2.4.225 Spherical quantum dot.

We assume that the barriers at the QD boundaries are infinite. The potential inside the QD is assumed to be 0 eV. We use a grid resolution of 0.5 nm. We solve the single-band Schrödinger equation within the effective-mass approximation. The electron effective mass of CdSe is assumed to be \(m_e = 0.112 m_0\).

A spherically symmetric potential leads to an energy spectrum where some eigenvalues are degenerate. We want to study the “shell structure” (degeneracy scheme) of a CdSe quantum dot of radius 5 nm. Figure 2.4.226 shows the calculated energy spectrum for the lowest 20 electron eigenvalues. One can clearly identify the shell structure 1s, 2p, 3d, 2s, 4f and 3p which is similar to the shell structure of the periodic table. This is the reason why quantum dots are often called “artificial atoms”. Note that each eigenstate is two-fold degenerate due to spin. Thus, the s states are two-fold degenerate, the p states are six-fold degenerate, the d states are ten-fold degenerate and the degeneracy of the f states is 14.

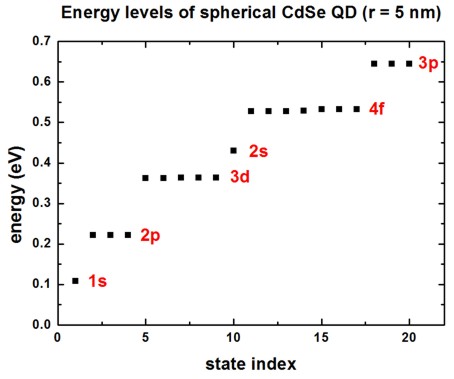
Figure 2.4.226 Eigenenergies of the lowest 20 states in the QD.

We have also solved the single-band Schrödinger equation for the holes assuming an isotropic effective mass for simplicity. Obviously, this is a crude approximation. From the electron and hole wave functions, we calculate their spatial overlap matrix elements (interband matrix elements). In this simple model, due to symmetry arguments, only the following transitions are allowed: 1s - 1s, 2p - 2p, 3d - 3d, 2s - 2s, 4f - 4f, …

Figure 2.4.227 shows the calculated interband matrix elements as a function of energy. (Note: The figure has to be updated: Now we output the square of this matrix element.)

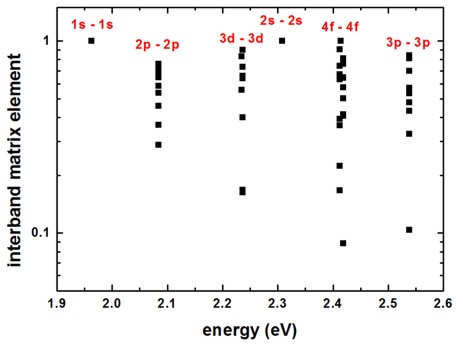
Figure 2.4.227 Interband matrix elements.

Both figures are in reasonable agreement with Fig. 1 and Fig. 2 (inset) in [Ferreira2006].

Energy levels of an “artificial atom” - Ellipsoidal, cigar-shaped CdSe quantum dot

For an ellipsoidal, cigar-shaped CdSe quantum dot (\(r_x = 5~\mathrm{nm}\), \(r_y = 5~\mathrm{nm}\), \(r_z = 10\mathrm{nm}\)), we calculate the lowest 30 eigenvalues.

Figure 2.4.228 Ellipsoidal quantum dot.

The energy spectrum (degeneracy spectrum) looks very different from the spherical QD spectrum (c.f. Figure 2.4.229)

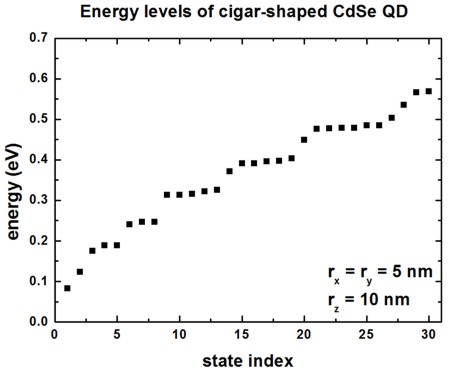
Figure 2.4.229 Eigenenergies of the lowest 30 states in the QD.

The interband matrix elements are shown in Figure 2.4.230 (Note: The figure has to be updated: Now we output the square of this matrix element.)

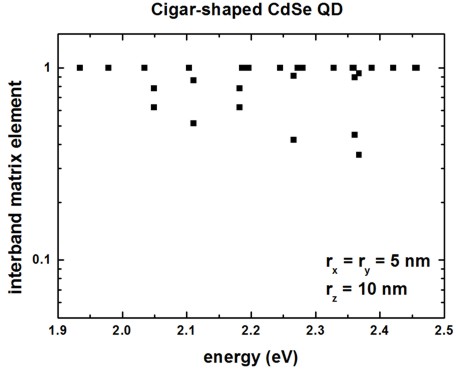
Figure 2.4.230 Interband matrix elements.

Energy levels of an “artificial atom” - 2D harmonic potential

The following figure shows the energy spectrum of a “two-dimensional disc” which we approximate as a cylindrically symmetric parabolic (harmonic) potential. We solve the 2D Schrödinger equation for this system. The harmonic potential is assumed to be \(\hbar\omega = 3~\mathrm{meV}\). Each shell is thus separated by 3 meV. From the energy spectrum of this two-dimensional shell structure, one can derive “magic numbers”. (They include spin degeneracy.)

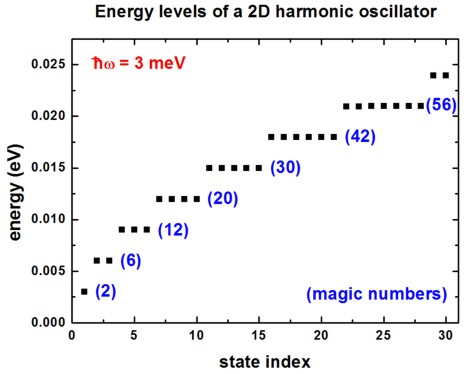
Figure 2.4.231 Eigenenergies of the lowest 30 states in a harmonic potential.

Version of this tutorial for nextnano³ can be found here .

Last update: 17/07/2024