Single-electron transistor - laterally defined quantum dot

Input files:

• SET_Scholze_IEEE2000_1D_nnpp.in

• SET_Scholze_IEEE2000_3D_cl_nnpp.in

• SET_Scholze_IEEE2000_3D_top_gates_cl_nnpp.in

Note

If you want to obtain the input files that are used within this tutorial, please check if you can find them in the installation directory. If you cannot find them, please submit a Support Ticket.

Scope:

In this tutorial, we simulate an \(AlGaAs\)/ \(GaAs\) heterostructure grown along the z direction. The tutorial is based on [Scholze2000].

Introduction

The \(AlGaAs\)/ \(GaAs\) heterostructure leads to a two-dimensional electron gas (2DEG). By applying a gate voltage on top of the structure in the (\(x\), \(y\)) plane, one is able to deplete the 2DEG and a laterally defined QD is formed. By adjusting the gate voltage, one is able to tune the number of electrons that are inside the QD.

Figure 2.5.15.59 shows the conduction band edge \(E_\mathrm{c}\) (\(x\), \(y\)) and the electron density \(n(x,y)\) for the 2DEG plane, i.e. at \(z\) = 8 nm below the \(GaAs\)/ \(AlGaAs\) heterojunction.

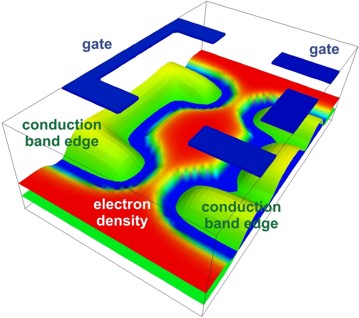
Figure 2.5.15.59 Conduction band edges (green), electron density (red) and geometry of the top gates (blue).

We divide the tutorial into two parts:

• In part 1, we simulate the heterostructure along the \(z\) direction and neglect the gates. (1D simulation: self-consistent Schrödinger-Poisson equation), SET_Scholze_IEEE2000_1D_nnpp.in

• In part 2, we solve the 3D Poisson equation to study the effect of the gates. (3D simulation: only Poisson equation using a classical density), SET_Scholze_IEEE2000_3D_top_gates_cl_nnpp.in

Part 1: 1D simulation (self-consistent Schrödinger-Poisson)

Figure 2.5.15.60 shows the calculated conduction band edge and the electron density of the heterostructure. The results are similar to Fig. 4 in [Scholze2000].

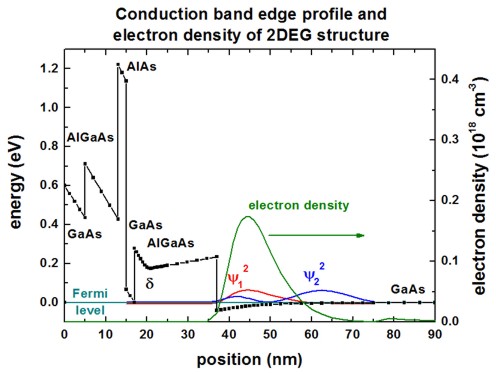
Figure 2.5.15.60 Conduction band edge profile (black), electron density (green) and Fermi levels (cyan) of 1D simulation.

At the left boundary, a Schottky barrier of 0.6 V has been assumed. At \(z\) = 20 nm, a \(\delta\)-doping layer is present. The Fermi level is assumed to be constant at \(E_\mathrm{F}\) = 0 eV. The ground state wave function (\(\Psi_1\)) is ~8 meV below the Fermi level and dominates the electron density. The first excited state (\(\Psi_2\)) is ~3 meV above the Fermi level, the second excited state (not shown) is 19 meV above the Fermi level.

Part 2: 3D simulation with top gates (Poisson equation only)

Figure 2.5.15.61 shows the 3D structure that we are going to simulate.

Figure 2.5.15.61 Device structure (3D)

Figure 2.5.15.62 shows two 2D slices through the lateral \((x,y)\) plane at a distance of 8 nm below the \(AlGaAs\)/ \(GaAs\) interface. The results are similar to Fig. 5 in [Scholze2000]. At the top, the four gates are shown.

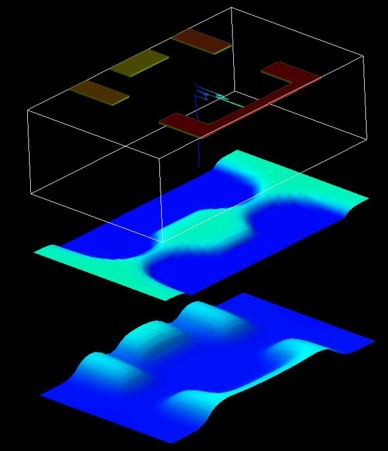
Figure 2.5.15.62 In the middle, the electron density is shown. The electron density has been calculated classically. At the bottom, the conduction band edge is shown.

Last update: nn/nn/nnnn