— DEV — Efficient method for the calculation of ballistic quantum transport - The CBR method (2D example)¶
Attention
This tutorial is under construction
Header¶
- Input Files:
Transmission_CBR_Mamaluy_JAP_2003_2D_nnp.in
Transmission_CBR_Mamaluy_JAP_2003_2D_holes_nnp.in
- Scope of the tutorial:
- Main adjustable parameters in the input file:
parameter
- Relevant output files:
bias_00000\bandedges.fld
bias_00000\Quantum\probabilities_shift_device_Gamma.fld
bias_00000\Quantum\probabilities_shift_lead_X_Gamma.dat
bias_00000\CBR\transmission_device_Gamma.dat
Introduction¶
In this tutorial, we apply the Contact Block Reduction (CBR) method to a Aharonov-Bohm-type structure with a large barrier in the middle of the device. This tutorial is based on [MamaluyCBR2003] and [BirnerCBR2009]. The input file Transmission_CBR_Mamaluy_JAP_2003_2D_holes_nnp.in simulates holes instead of electrons.
Simulation setup¶
First, we look into the structure of the device. Figure 2.4.14.19 shows the calculated conduction band edge of the device.
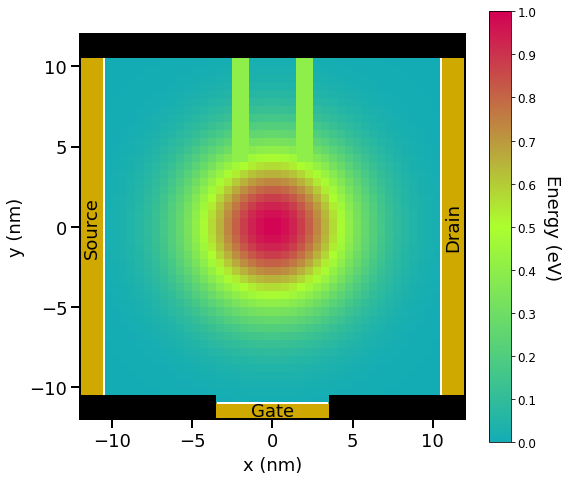
Figure 2.4.14.19 The calculated conduction band edge. The center of the device \(\left((x, y) = (0, 0)\;\mathrm{(nm)}\right)\) is AlAs and the energy is \(1.0\;\mathrm{(eV)}\). The vicinity of the edges of the device is GaAs and the energy is \(0\;\mathrm{(eV)}\). The double potential barrier is set so that the energy is equivalent to \(0.4\;\mathrm{(eV)}\). Note that the blacked out areas are set up with barriers of infinite height. bias_00000\bandedges.fld¶
The image below shows the 3-dimenional conduction band edge. Note that the height of the infinite potential barriers are set to \(2.0\;\mathrm{(eV)}\) for convenience.
Figure 2.4.14.20 Potential landscape¶
This device has some features.
The device consists of three contacts that are called ‘source’, ‘gate’ and ‘drain’. They also have leads adjacent to them, indicated by white lines in Figure 2.4.14.19
In the middle of the device a potential barrier of two-dimensional Gaussian shape effectively expels the electrons from the center. The energy profile is given by
where \(E_{c,0} = 1.0\;\mathrm{(eV)}\) so that the maximum height of the Gaussian barrier becomes \(1.0\;\mathrm{(eV)}\) at the center of the device. In this tutorial, \(a\;=\; 5\;\mathrm{(nm)}\).
In the upper part of the device, a thin tunneling double barrier is present and the height is \(0.4\;\mathrm{(eV)}\).
These conduction band profiles are achieved by adjusting the database{ } as below.
database{
binary_zb{
name = "GaAs"
conduction_bands{ Gamma{ mass = 0.3 bandgap = 0 } # effective mass 0.3m0
valence_bands{
bandoffset = 0.0 # artificially shifted so that (GaAs conduction bandedge) = 0.0 eV
delta_SO = 0.0
}
}
binary_zb{
name = "AlAs"
conduction_bands{ Gamma{ mass = 0.3 bandgap = 0 } # effective mass 0.3m0
valence_bands{
bandoffset = 1.00 # artificially shifted so that (AlAs conduction bandedge) = 1.0 eV
delta_SO = 0.0
}
}
bowing_zb{
name = "AlGaAs_Bowing_x"
valence = III_V
conduction_bands{ Gamma{ mass = 0.0 bandgap = 0.000 } } # bowing is switched off for this simulation
valence_bands{
bandoffset = 0.000 # artificially shifted so that (Al0.4Ga0.6As conduction bandedge) = 0.4 eV
delta_SO = 0
}
}
bowing_zb{
name = "AlGaAs_Bowing_1_x"
valence = III_V
conduction_bands{ Gamma{ mass = 0.0 bandgap = 0.000 } } # bowing is switched off for this simulation
valence_bands{
bandoffset = 0.000 # artificially shifted so that (Al0.4Ga0.6As conduction bandedge) = 0.4 eV
delta_SO = 0
}
}
ternary2_zb {
name = "Al(x)Ga(1-x)As"
valence = III_V
binary_x = AlAs
binary_1_x = GaAs
bowing_x = AlGaAs_Bowing_x
bowing_1_x = AlGaAs_Bowing_1_x
}
}
In addition, the infinite potential barriers surround the device as shown as blacked out areas in Figure 2.4.14.19.
The effective electron mass is assumed to be constant throughout the device and equal to \(0.3m_{0}\).
We set the boundary conditions as follows:
If it is at the boundary, and if it is in contact to a lead, a Neumann boundary condition is set.
If it is at the boundary, and if it is not in contact to a lead, a Dirichlet boundary condition is set.
quantum{
region{
name = "device"
no_density = yes
x = [ $x_contact_left, $x_contact_right ]
y = [ $y_contact_bottom, $y_quantum_top ]
boundary{ x = neumann y = neumann } # boundary condition for CBR = Neumann for propagation direction & Dirichlet for perpendicular direction.
Gamma{ num_ev = $num_eigenstates_device cutoff = 4.0 }
output_wavefunctions{
probabilities = yes
max_num = $num_output_wavefunctions_device
in_one_file = no
}
}
# lead 1 is a 1D line (x = $contact_left).
region{
name = "lead_1"
no_density = yes
x = [ $x_contact_left, $x_contact_left ]
y = [ $y_inf_barrier_bottom, $y_inf_barrier_top ]
boundary{ x = neumann y = dirichlet }
Gamma{ num_ev = $num_eigenstates_lead1 cutoff = 4.0 }
output_wavefunctions{ probabilities = yes max_num = $num_eigenstates_lead1 }
}
# lead 2 is a 1D line (y = $y_contact_bottom).
region{
name = "lead_2"
no_density = yes
x = [ $bottom_contact_left, $bottom_contact_right ]
y = [ $y_contact_bottom, $y_contact_bottom ]
boundary{ x = dirichlet y = neumann }
Gamma{ num_ev = $num_eigenstates_lead2 cutoff = 4.0 }
output_wavefunctions{ probabilities = yes max_num = $num_eigenstates_lead2 }
}
# lead 3 is a 1D line (x = $x_contact_right).
region{
name = "lead_3"
no_density = yes
x = [ $x_contact_right, $x_contact_right ]
y = [ $y_inf_barrier_bottom, $y_inf_barrier_top ]
boundary{ x = neumann y = dirichlet }
Gamma{ num_ev = $num_eigenstates_lead3 cutoff = 4.0 }
output_wavefunctions{ probabilities = yes max_num = $num_eigenstates_lead3 }
}
cbr{
name = "device"
lead{ name = "lead_1" }
lead{ name = "lead_2" }
lead{ name = "lead_3" }
delta_energy = 0.0005 # energy resolution
min_energy = 0.0 # minimum energy
max_energy = 0.5 # maximum energy
}
}
Note the following points.
To consistent with the results of [MamaluyCBR2003] and [BirnerCBR2009], the quantum region is extended (1 grid point outside along x and y direction), respect to the device dimensions in the papers.
This is attributed to the difference in the way boundary conditions are set in nextnano++ and nextnano³. The details are described below in attention.
To set dirichlet boundary conditions at the top and bottom of the device that are no contact with leads, the quantum region is extended to the infinite potential barrier (1 grid point further outside along y direction), respect to the device dimensions in the papers.
The difference in the device dimensions from in [MamaluyCBR2003] and [BirnerCBR2009] arise from the reasons above.
For each energy \(E\) (energy step is equal to 0.0005) where the transmission coefficient \(T(E)\) has to be calculated, a matrix of size 95 \(\mathrm{\times}\) 95 has to be inverted. The size of 95 is determined by the sum of the number of grid points in each lead that are in contact to the device.
Lead 1 (Source): 41 grid points
Lead 2 (Gate): 13 grid points
Lead 3 (Drain): 41 grid points
in total: 95 grid points
The total CPU time for calculation of the transmission \(T(E)\) in this example is about 5 seconds for 303 eigenstates.
Note that we do not take into account the increase in grid points due to the increase in the gate length.
Transmission¶
Figure 2.4.14.21 shows the calculated transmission coefficients of the various lead combinations \(T_{12}\), \(T_{23}\), and \(T_{13}\). For the orange-dashed lines 100 % (1681 of 1681) of all eigenvectors were used whereas for the light-blue lines only 18 % (303 of 1681) had to be calculated. You can see that reducing the eigenvectors to 18 % or even 7 % (118 of 1681) of the total eigenvectors does not result in significant changes in \(T(E)\), especially at lower energies. This means that one does not have to calculate all eigenvalues of the device Hamiltonian which grossly reduces CPU time. A small percentage of eigenvalues suffices for \(T(E)\) in relevant energy range of interest.
Figure 2.4.14.21 The transmission coefficient \(T(E)\) of a 2D sample with 3 leads. \(T_{12}\) in (a), whereas \(T_{13}\) in (b). bias_00000\CBR\transmission_device_Gamma.dat¶
The nextnano++ results differ slightly from the [MamaluyCBR2003] and [BirnerCBR2009].
- Reasons:
The potential energy profile in the device and in the leads is not identical, as well as the dimensions of the barriers.
The dimensions of the device are not identical as explained (See the attention below for further information).
Therefore, the eigenenergies and the wave functions in the device, and in the leads differ slightly which explains the small deviations.
The 16th eigenstate is a resonance state of the lower transmission path.
1st resonance: the 16th eigenstate: \(0.119\;\mathrm{(eV)}\)
The square of the 16th wave function with the conduction band is shown below. (bias_00000\Quantum\probabilities_shift_device_Gamma.fld)
Figure 2.4.14.22 The 16th eigenstate¶
Note that the square of the wave function is rescaled so that you can see the shape clearly.
The 26th eigenstate and 29th eigenstate are resonance states of the double barrier.
1st resonance:
the 26th eigenstate: \(0.177\;\mathrm{(eV)}\) (delocalized)
the 29th eigenstate: \(0.193\;\mathrm{(eV)}\) (more localized)
2nd resonance:
the 56th eigenstate: \(0.311\;\mathrm{(eV)}\) (delocalized)
the 59th eigenstate: \(0.328\;\mathrm{(eV)}\) (more localized)
the 61th eigenstate: \(0.336\;\mathrm{(eV)}\) (delocalized)
the 63th eigenstate: \(0.347\;\mathrm{(eV)}\) (delocalized)
the 64th eigenstate: \(0.352\;\mathrm{(eV)}\) (more localized)
TO BE CHECKED
The follow figure shows the square of the wave function of the 26th eigenstate with the conduction band. (bias_00000\Quantum\probabilities_shift_device_Gamma.fld) You can clearly see that it is a resonance state of the double barrier and corresponds to the second peak in the light-blue transmission curve \(T_{13}\) from source to draian around \(190\;\mathrm{(meV)}\).
Figure 2.4.14.23 The 26th eigenstate¶
Note that the square of the wave function is rescaled so that you can see the shape clearly.
Lead modes¶
Figure 2.4.14.24 shows the lead modes of the gate, and the source (which is identical to the drain). In the transmission curve \(T_{12}(E) = T_{23}(E)\), the transmisson shows a step-like behavior which is related to the energies of lead 2 (‘gate’).
Figure 2.4.14.24 The lead modes of lead 2 (‘gate’) are shown in (a), whereas the lead modes of lead 1, 3 (‘source’, ‘drain’) are shown in (b). bias_00000\Quantum\probabilities_shift_lead_X_Gamma.dat¶
Notes¶
Attention
Here the difference in the way of setting up boundary conditions in nextnano++ and nextnano³ will be discussed.
Last update: nn/nn/nnnn