Mobility in two-dimensional electron gases (2DEGs)
Author: Stefan Birner
The input files used in this tutorial are:
1DInSb_mobility_ShaoFig3.in
1DGaAs_mobility_WalukiewiczFig2.in
1DGaAs_mobility_WalukiewiczFig3.in
1DInGaAs_mobility_WalukiewiczFig8.in
1DGaN_mobility_WalukiewiczFig4.in
1DGaN_mobility_WalukiewiczFig5.in
Table of Contents
Mobility in delta-doped InSb quantum wells
This tutorial is based on the following paper:
Carrier Mobilities in delta-doped Heterostructures, Y. Shao, S.A. Solin, L.R. Ram-Mohan, arXiv: Materials Science (2006)
Our implementation is based on the equations that are given in this paper (with the exception of Eq. (3.5) where we added a factor of \(\frac{1}{4 \pi}\) because of SI units).
We calculate the mobility in a 40 nm InSb quantum well that is surrounded by and strained with respect to Al0.15In0.85Sb barriers.
At z = -20 nm, there is a delta-doping layer with a sheet doping density of \(1 \times 10^{12} \text{cm}^{-2}\). The delta-doping layer is separated from the InSb QW by a 40 nm Al0.15In0.85Sb spacer layer.
quantum-well-width = 40.0 ! [nm] [Shao] Fig. 3
spacer-width = 40.0 ! [nm] [Shao] Fig. 3
remote-doping-sheet-density = 1e12 ! [cm^-2] [Shao] Fig. 3
We calculate all properties for different temperatures. This can be done as follows:
$global-parameters
lattice-temperature = 1.0 ! start value T = 1 [K]
temperature-sweep-active = yes ! 'yes' / 'no'
temperature-sweep-step-size = 10.0 ! increase temperature each time by T = 10 [K]
temperature-sweep-number-of-steps = 31 ! increase temperature 31 times
data-out-every-nth-step = 1 ! output all data for every temperature sweep
$end_global-parameters
All output files are labelled with an index, starting from zero, that refers to each individual temperature sweep: .../..._ind000....dat
Here, the index runs from 0 (000) to 30 (030), i.e. 31 output files for each property in total.
We note that band gaps and lattice constants depend on temperature. This is taken into account automatically for each temperature sweep. The following figure shows the conduction band edge, the Fermi level and the square of the lowest two electron wave functions at T = 1 K.
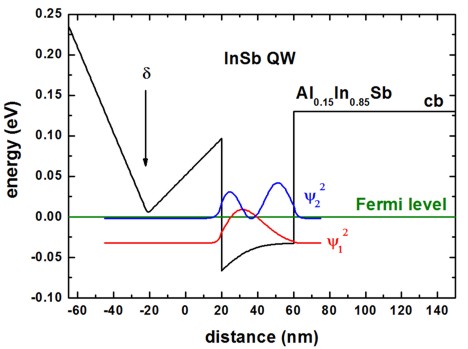
To plot such a figure, the following output files are needed:
band_structure/cb1D_001_ind000.dat1st column: distance [nm]
2nd column: conduction band edge at the Gamma point [eV]
Note: The index ‘ind000’ refers to the temperature sweep. Here, index 0 means T = 1 K.
current/fermi1Del_ind000.dat1st column: distance [nm]
2nd column: Fermi level of the electrons [eV]
In this tutorial, the Fermi level is always equal to 0 eV.
Schroedinger_1band/cb001_ind000_sg1_deg1.dat1st column: distance [nm]
n columns: n energies of the eigenstates [eV]
n columns: n squares of the wave functions (\(\psi ^2\)) [eV]
In the figure, we plotted the columns for \(\psi ^2\) of the two lowest states: \(\color{red}{\psi_1 ^2}\), \(\color{blue}{\psi_2 ^2}\)
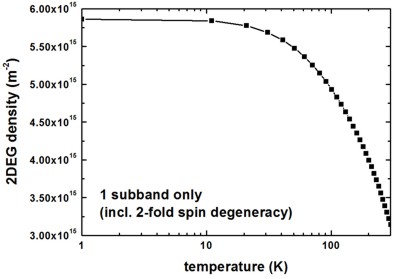
The following figure shows the sheet electron density as a function of temperature. We considered the two lowest subbands for calculating the 2DEG density (the spin degeneracy of the subbands is included):
2DEG-sheet-density-number-of-subbands = 2
Our results differ from the results of Fig. 3(b) of the Shao’s paper. (Some obvious discrepancies are the conduction band offset (We used ~0.15 eV whereas Shao used ~0.25 eV.) and the Schottky barrier height.)
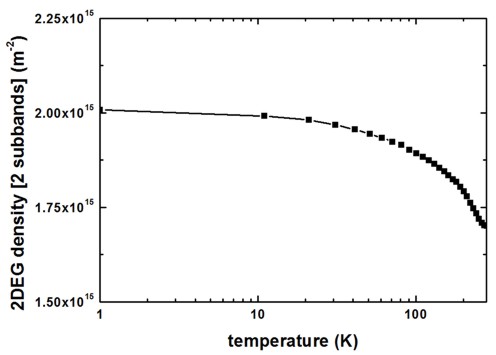
To plot such a figure, the following output file was used:
Monte_Carlo/mobility_TemperatureSweep.dat1st column: temperature [K]
last column: electron sheet density of the lowest subband(s) [m^-2]
The following figure shows the calculated 2DEG mobility as a function of temperature. The relevant data can be found in this file:
Monte_Carlo/mobility_TemperatureSweep.dat1st column: temperature [K]
2nd column: total mobility [m2/Vs]
3rd column: mobility due to ionized impurity scattering [m2/Vs]
4th column: mobility due to background impurity scattering [m2/Vs]
5th column: mobility due to deformation potential acoustic phonon scattering [m2/Vs]
6th column: mobility due to polar optic (LO) phonon scattering [m2/Vs]
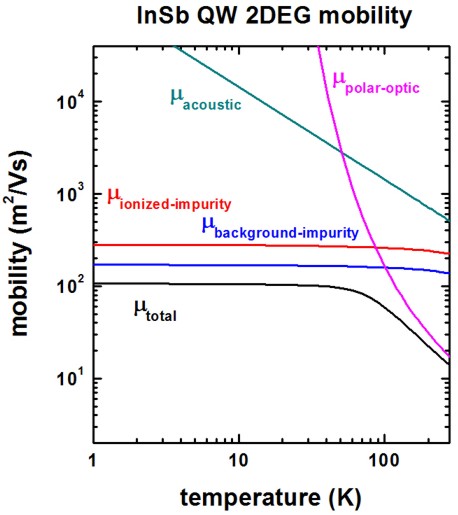
We included the following scattering mechanisms:
ionized-impurity-scattering = yes ! [Shao] (including remote and background ionized impurity scattering)
acoustic-phonon-scattering = yes ! [Shao]
polar-optical-phonon-scattering = yes ! [Shao]
alloy-scattering = no ! [Shao]
We now discuss the agreement/disagreement compared to Fig. 3(a) of the [Shao] paper.
The mobility due to acoustic phonon scattering is in excellent agreement.
The mobility due to polar optic LO phonon scattering is in excellent agreement if one takes into account that [Shao] forgot to include the factor of 1/(4 pi) due to SI units.
The mobility due to ionized and background impurity scattering differs significantly. It seems that the disagreement is not only due to the different sheet density that has been used. We used the following value
impurity-background-doping-concentration = 5e15 ! [cm^-3] [Shao] Fig. 3
The following InSb material parameters have been used:
conduction-band-masses = 0.0135 0.0135 0.0135 ! [m0] [Shao]
... !
static-dielectric-constants = 16.82 16.82 16.82 ! [Shao] epsilon(0)
optical-dielectric-constants = 15.7 ! [Shao] epsilon(infinity)
LO-phonon-energy = 0.025 ! [eV] [Shao] (optical phonon energy)
mass-density = 5.79e3 ! [kg/m^3] [Shao]
sound-velocity = 3.7e3 ! [m/s] [Shao]
acoustic-deformation-potential = 7.2 ! [eV] [Shao]
Mobility in doped GaAs quantum wells
The following input files were used:
1DGaAs_mobility_WalukiewiczFig2.in (Experiment of Hiyamizu et al.)
1DGaAs_mobility_WalukiewiczFig3.in (Experiment of DiLorenzo et al.)
Here, we test our algorithm to results on GaAs 2DEGs of another publication. We note that our algorithm is suitable for delta-doped 2DEGs but the GaAs examples are not delta-doped.
This section is based on the following paper:
The experimental data is baed on:
Conduction band profile and wave functions
[Walukiewicz, Fig. 2]: [Hiyamizu]
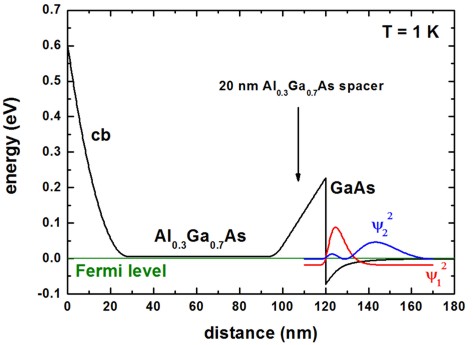
! 20 nm Al0.3Ga0.7As spacer
spacer-width = 20.0 ! 20 [nm]
[Walukiewicz, Fig. 3]: [DiLorenzo]
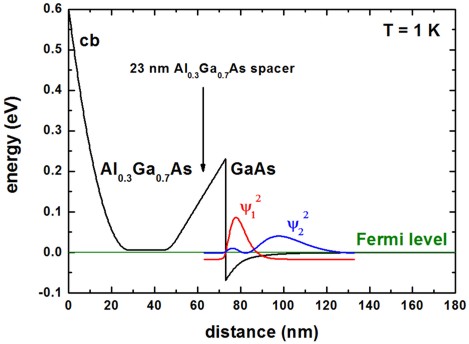
! 23 nm Al0.3Ga0.7As spacer
spacer-width = 23.0 ! 23 [nm]
2DEG sheet density
[Walukiewicz, Fig. 2]: [Hiyamizu]
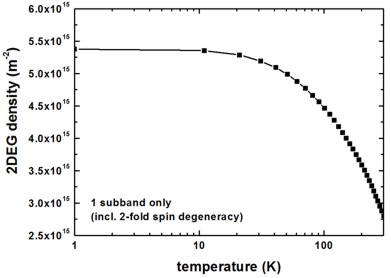
[Walukiewicz, Fig. 3]: [DiLorenzo]
Mobility
[Walukiewicz, Fig. 2]: [Hiyamizu]
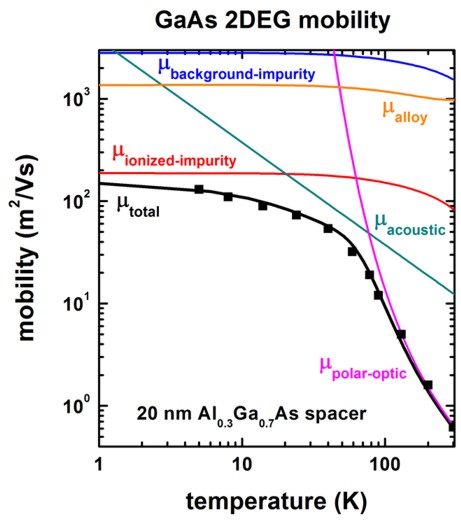
impurity-background-doping-concentration = 9e13 ! [cm-3]
remote-doping-sheet-density = 3.5e11 ! [cm-2] (to fit experiment)
(remote-doping-sheet-density = 1.948344e11 ! [cm-2])
![Walukiewicz] Fig. 2: 8.6 * 1016 [cm-3] ==> 8.6 * 1016 [cm-3]2/3 = 1.948344e11 (?)
[Walukiewicz, Fig. 3]: [DiLorenzo]
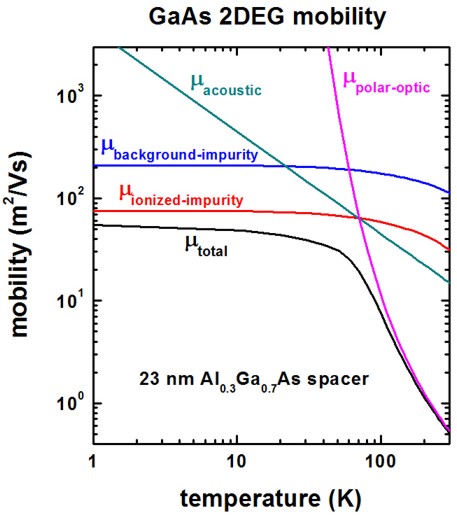
impurity-background-doping-concentration = 1e15 ! [cm-3]
remote-doping-sheet-density = 1e12 ! [cm-2]
Differences with respect to Walukiewicz [Hiyamizu] paper
Walukiewicz used a 2DEG density of \(3 \times 10^{11} \text{cm}^{-2}\).
conduction-band-masses = 0.067 0.067 0.067 ! [m0]
... ! a higher value than for bulk because of nonparabolicity
Here we used 0.067 as this gives better agreement to the mobility at higher temperatures and this is the usually accepted material parameter for GaAs.
quantum-well-width = 13.0 ! [nm] (13 nm seems to be a better value than 20 nm.)
alloy-scattering = yes
Alloy scattering is relevant for the part of the wave function that penetrates into the AlGaAs barrier.
The squares are experimental values of Fig. 5 in:
The following GaAs material parameters have been used:
static-dielectric-constants = 12.9 12.9 12.9 ! [Walukiewicz] epsilon(0)
optical-dielectric-constants = 10.9 ! [Walukiewicz] epsilon(infinity)
LO-phonon-energy = 0.036 ! [eV] [Walukiewicz] (optical phonon energy)
mass-density = 5.318e3 ! [kg/m^3] [Davies] p. 411
sound-velocity = 5.29e3 ! [m/s] [X.L. Lei, J. Phys. C 18, L593 (1985)]
acoustic-deformation-potential = 7.0 ! [eV] [Walukiewicz]
Into the equation for the deformation potential acoustic phonon scattering, the quantum well width is an input parameter. We used a value of 13 nm which corresponds roughly to the extension of the ground state wave function inside the “triangular” QW.
Differences with respect to Walukiewicz [DiLorenzo] paper
In Walukiewicz’s paper, the background impurity scattering is dominating the ionized impurity scattering. We found the opposite.
Walukiewicz used a 2DEG density of \(2.2 - 3.8 \times 10^{11} \text{cm}^{-2}\)
conduction-band-masses = 0.076 0.076 0.076 ! [m0] [Walukiewicz]
... ! a higher value than for bulk because of nonparabolicity. This is also the value used by Walukiewicz.
quantum-well-width = 20.0 ! [nm] (This value might be too large. See left where 13 nm was used.)
alloy-scattering = no
Mobility in doped InGaAs quantum wells
The input file used is:
1DInGaAs_mobility_WalukiewiczFig8.in (Experiment of Kastalsky et al.)
Here, we test our algorithm to results on InGaAs 2DEGs of another publication. We note that our algorithm is suitable for delta-doped 2DEGs but the InGaAs examples are not delta-doped.
This tutorial is based on the following paper:
The experimental data is based on:
[Kastalsky] and [Walukiewicz] have used In0.52Al0.48As whereas we used In0.52Al0.48As which is lattice matched to InP and In0.53Al0.47As.
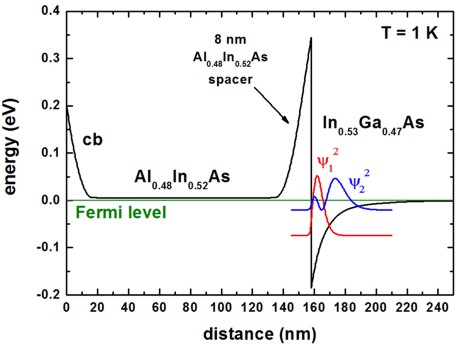
The conduction band profile is shown in the following figure. Here, two subbands (\(\color{red}{\psi_1 ^2}\), \(\color{blue}{\psi_2 ^2}\)) are occupied although our implementation of calculating the mobility is only applicable to one occupied subband. Note that the 2DEG is located in an alloy, i.e. InGaAs. Thus we expect that alloy scattering has a significant effect on the total mobility.
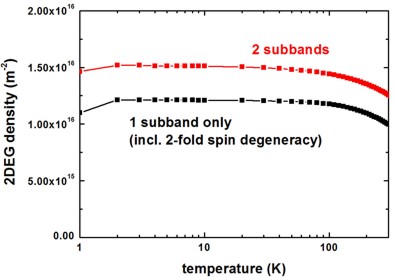
The following figure shows the subband density of the first subband and of the first two subbands as a function of temperature. Inside the mobility algorithm, only the density of the first subband has been considered.
The following figure shows the mobility as a function of temperature. At temperatures below 100 K, the total mobility is dominated by alloy scattering.
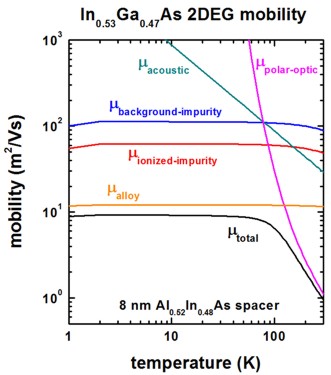
Our results for the mobility are in reasonable agreement with Fig. 8 of the paper of [Walukiewicz].
The following parameters were used:
ionized-impurity-scattering = yes ! (including remote and background ionized impurity scattering)
acoustic-phonon-scattering = yes !
polar-optical-phonon-scattering = yes !
alloy-scattering = yes !
quantum-well-width = 15.0 ! [nm] 15 nm seems to be a reasonable approximation for the triangular well
spacer-width = 8.0 ! [nm]
impurity-background-doping-concentration = 1.0e16 ! [cm-3]
remote-doping-sheet-density = 1.0e12 ! [cm-2]
2DEG-sheet-density-number-of-subbands = 1
alloy-disorder-scattering-potential = 0.60 ! [eV] InGaAs bulk value [J.R. Hayes et al. (1982)]
!----------------------------------------------------------------------------
! In0.53Ga0.47As material parameters
!----------------------------------------------------------------------------
mass-density = 5.5025e3 ! [kg/m^3] InGaAs [Wen et al., JAP 100, 103516 (2006)]
sound-velocity = 4.753e3 ! [m/s] In0.53Ga0.47As[111] [Wen et al., JAP 100, 103516 (2006)]
acoustic-deformation-potential = 7.0 ! [eV] InGaAs [Walukiewicz]
Mobility in doped GaN quantum wells
The input files used are:
1DGaN_mobility_WalukiewiczFig4.in
1DGaN_mobility_WalukiewiczFig5.in
Here, we test our algorithm to results on GaN 2DEGs of another publication. We note that our algorithm is suitable for delta-doped 2DEGs but the GaN examples are not delta-doped.
This tutorial is based on the following paper:
Note: To be consistent with the paper of Walukiewicz, no (!) piezo- and pyroelectricity is included.
The following GaN material parameters have been used:
conduction-band-masses = 0.21 0.21 0.21 ! [m0] [WalukiewiczGaN]
static-dielectric-constants = 9.5 9.5 9.5 ! [WalukiewiczGaN] epsilon(0)
optical-dielectric-constants = 5.35 5.35 5.35 ! [WalukiewiczGaN] epsilon(infinity)
LO-phonon-energy = 0.0905 0.0905 0.0905 ! [eV] [WalukiewiczGaN] (optical phonon energy)
mass-density = 6.1e3 ! [kg/m^3] [WalukiewiczGaN]
sound-velocity = 6.6e3 ! [m/s] [WalukiewiczGaN]
acoustic-deformation-potential = 8.5 ! [eV] [WalukiewiczGaN]
alloy-disorder-scattering-potential = 2.3 ! [eV] conduction band offset GaN/AlN
Here, alloy scattering is only relevant for the part of the wave function that penetrates into the AlGaN barrier.
Conduction band profile and wave functions [WalukiewiczGaN]
[WalukiewiczGaN] Fig. 4
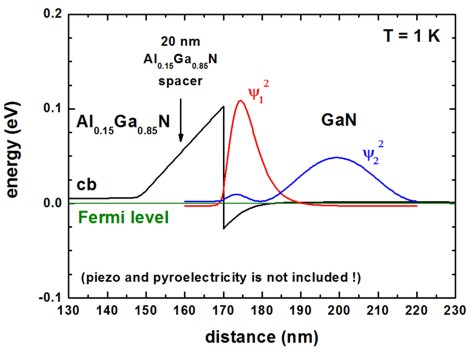
! 20 nm Al0.15Ga0.85N spacer
spacer-width = 20.0 ! 20 [nm]
[WalukiewiczGaN] Fig. 5
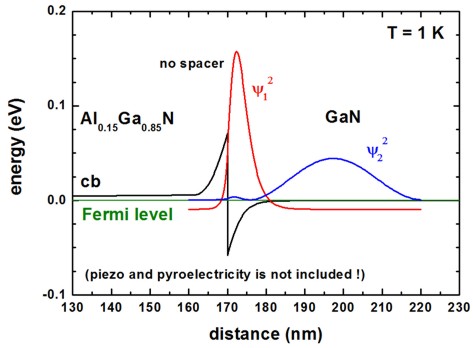
! no spacer
spacer-width = 0.0 ! 0 [nm]
2DEG sheet density
[WalukiewiczGaN] Fig. 4
Into the equation for the deformation potential acoustic phonon scattering, the quantum well width is an input parameter. We used values which correspond roughly to the extension of the ground state wave function inside the “triangular” QW.
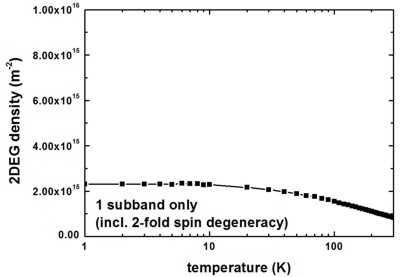
[WalukiewiczGaN] used a 2DEG density of 6.2 * 1015 m-2.
quantum-well-width = 15.0 ! 15 [nm]
[WalukiewiczGaN] Fig. 5
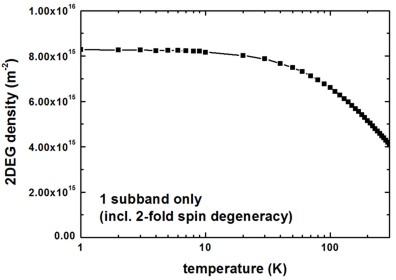
[WalukiewiczGaN] used a 2DEG density of 1.59 * 1016 m-2.
quantum-well-width = 10.0 ! 10 [nm]
Mobility
[WalukiewiczGaN] Fig. 4
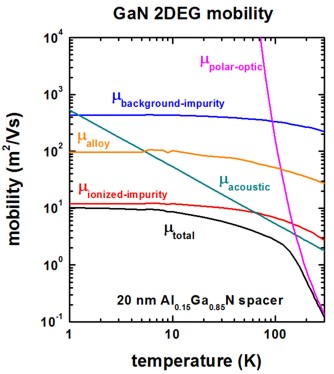
impurity-background-doping-concentration = 1e14 ! [cm-3]
remote-doping-sheet-density = 7.883735e11 ! [cm-2]
![WalukiewiczGaN] Fig. 4: 7 * 1017 [cm-3] ==> 7 * 1017 [cm-3]2/3
[WalukiewiczGaN] Fig. 5
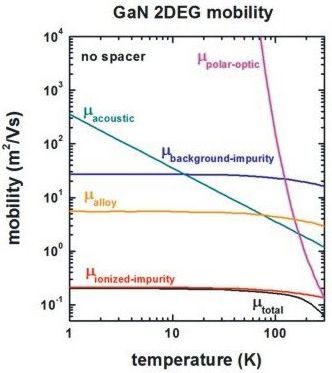
impurity-background-doping-concentration = 4e15 ! [cm-3]
remote-doping-sheet-density = 1e12 ! [cm-2]
Final remark: In principle, the results of these GaN 2DEGs are not reliable as piezo- and pyroelectricity have to be included. Our results disagree quantitatively with the results of [WalukiewiczGaN]. However, it is not clear, which material parametes he used for the conduction band offset and the alloy scattering.
Further hints
If two remote doping regions should be taken into account, one can input an array of values.
spacer-width = 20.0 10.0 ! [nm] spacer width of 1st and 2nd doping region
remote-doping-sheet-density = 1e12 1e11 ! [cm-2] remote doing density of 1st and 2nd doping region