nextnano3 - Tutorial
next generation 3D nano device simulator
3D Tutorial
Energy levels of an "artificial atom" - Spherical and ellipsoidal CdSe
Quantum Dot
Author:
Stefan Birner
If you want to obtain the input files that are used within this tutorial, please
check if you can find them in the installation directory.
If you cannot find them, please submit a
Support Ticket.
-> 3DsphericCdSeQD5nm_ArtificialAtom.in -
spherical CdSe QD with radius 5 nm
-> 3DsphericCdSeQD_ArtificialAtom_radius.in -
spherical CdSe QD with radius as a parameter
-> 3DellipsoidalCdSeQD5nm5nm10nm_ArtificialAtom.in -
ellipsoidal, cigar-shaped CdSe QD with radii 5 nm, 5nm and 10 nm
-> 2DGaAs_BiParabolicQW_3meV.in -
2D harmonic potential
Energy levels of an "artificial atom" - Spherical CdSe Quantum Dot
-> 3DsphericCdSeQD5nm_ArtificialAtom.in -
spherical CdSe QD with radius 5 nm
Here, we want to calculate the energy levels and the wave functions of a
spherical CdSe
quantum dot of radius 5 nm.

We assume that the barriers at the QD boundaries are infinite.
The potential inside the QD is assumed to be 0 eV.
We use a grid resolution of 0.5 nm.
We solve the single-band Schrödinger equation within the effective-mass
approximation.
The electron effective mass of CdSe is assumed to be me
= 0.112 m0.
conduction-band-masses = 0.026d0 0.026d0 0.026d0 ! electron
effective mass at Gamma conduction band
...
A spherically symmetric potential leads to an energy spectrum where some
eigenvalues are degenerate.
We want to study the "shell structure" (degeneracy scheme) of a CdSe quantum dot
of radius 5 nm.
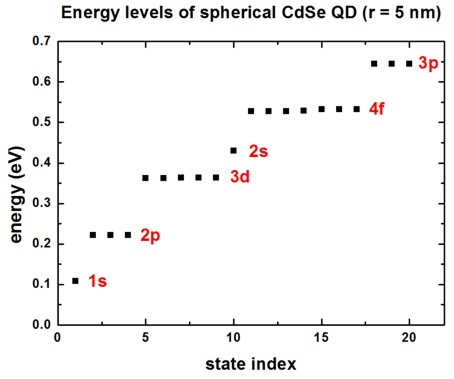
The following figure shows the calculated energy spectrum for the lowest 20
electron eigenvalues.
One can clearly identify the shell structure 1s, 2p, 3d, 2s, 4f and 3p which is
similar to the shell structure of the periodic table.
This is the reason why quantum dots are often called "artificial atoms".
Note that each eigenstate is two-fold degenerate due to spin.
Thus the s states are two-fold degenerate, the p
states are six-fold degenerate, the d states are ten-fold
degenerate and the degeneracy of the f states is 14.
We have also solved the single-band Schrödinger equation for the holes
assuming an isotropic effective mass for simplicity.
Obviously, this is a crude approximation.
From the electron and hole wave functions, we calculate their spatial overlap
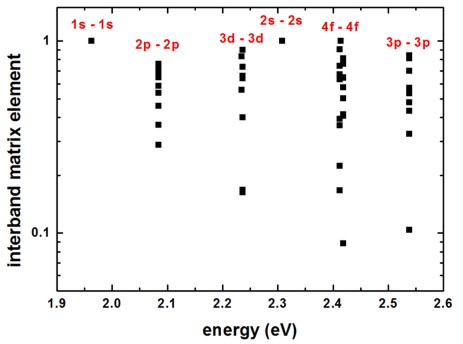
matrix elements (interband matrix elements).
In this simple model, due to symmetry arguments, only the following transitions
are allowed:
1s - 1s, 2p - 2p, 3d - 3d, 2s - 2s, 4f - 4f, ...
The following figure shows the calculated interband matrix elements as a
function of energy.
(Note: The figure has to be updated: Now we output the square of this matrix
element.)
Both figures are in reasonable agreement with Fig. 1 and Fig. 2 (inset) of the
following paper:
Optical Properties of Ellipsoidal CdSe Quantum Dots
W.S. Ferreira, J.S. de Sousa, J.A.K. Freire, G.A. Farias, V.N. Freire
Brazilian Journal of Physics 36, 438 (2006)
Energy levels of an "artificial atom" - Ellipsoidal, cigar-shaped CdSe
quantum dot
-> 3DellipsoidalCdSeQD5nm5nm10nm_ArtificialAtom.in -
ellipsoidal, cigar-shaped CdSe QD with radii 5 nm, 5nm and 10 nm
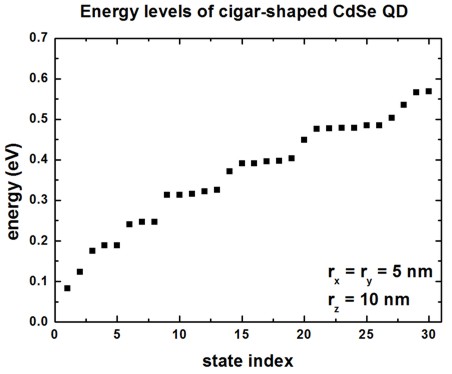
For an ellipsoidal, cigar-shaped CdSe quantum dot (rx = 5 nm, ry
= 5 nm, rz = 10 nm), we calculate the lowest 30 eigenvalues.

The energy spectrum (degeneracy spectrum) looks very different from the
spherical QD spectrum.
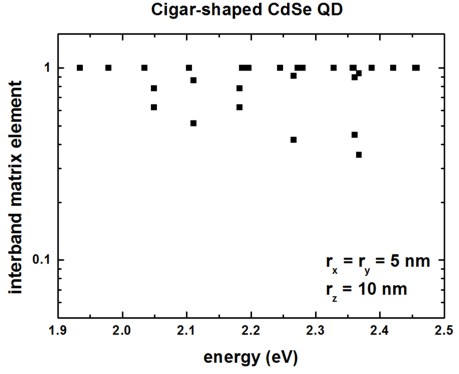
The interband matrix elements are shown in this figure:
(Note: The figure has to be updated: Now we output the square of this matrix
element.)
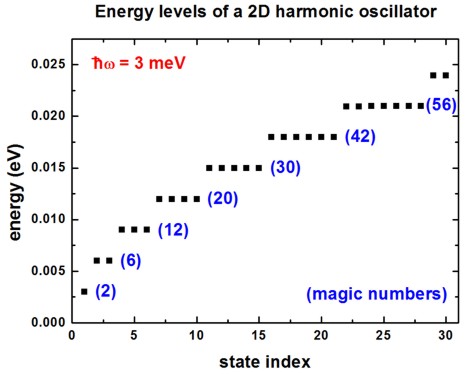
Energy levels of an "artificial atom" - 2D harmonic potential
-> 2DGaAs_BiParabolicQW_3meV.in -
2D harmonic potential
The following figure shows the energy spectrum of a "two-dimensional disc" which
we approximate as a cylindrically symmetric parabolic (harmonic) potential.
We solve the 2D Schrödinger equation for this system.
The harmonic potential is assumed to be hbarw = 3 meV. Each shell is
thus separated by 3 meV.
From the energy spectrum of this two-dimensional shell structure, one can derive
"magic numbers". (They include spin
degeneracy.)
See also this tutorial for two-dimensional parabolic confinement:
Fock-Darwin states
|