Landau levels of a bulk GaAs sample in a magnetic field¶
In this tutorial, we study the electron energy levels of a bulk GaAs sample that is subject to a magnetic field.
The input files are the followings:
2DBulkGaAs_LandauLevels_nn3.in / *_nnp.in
Simulation details¶
The magnetic field is oriented along the z direction. The motion in the z direction is not influenced by the magnetic field and is thus that of a free particle with energies and wave functions given by:
For that reason, we do not include the z direction into our simulation domain, and thus only simulate in the (x,y) plane (two-dimensional simulation).
This plane has the size of 300 nm \(\times\) 300 nm and consists of GaAs. At the domain boundaries we employ Dirichlet boundary conditions to the Schrödinger equation, i.e. infinite barriers.
We calculate the eigenstates for different magnetic field strengths (1 T, 2 T, 3 T).
global{
...
magnetic_field{
strength = $B # [T]
}
}
$magnetic-field
magnetic-field-on = yes
magnetic-field-strength = 0.0 ! 0 Tesla = 0 Vs/m2
magnetic-field-direction = 0 0 1 ! [001] direction
magnetic-field-sweep-active = yes !
magnetic-field-sweep-step-size = 1.0 ! 1 Tesla = 1 Vs/m2
magnetic-field-sweep-number-of-steps = 3 ! 3 magnetic field sweep steps
output-magnetic-vector-potential = yes ! output of A(x,y,z)
$end_magnetic-field
- Magnetic length and cyclotron frequency
A useful quantitiy is the magnetic length (or Landau magnetic length) which is defined as:
\[l_B = \left(\frac{\hbar}{m_e^* \omega_c}\right)^{1/2} = \left(\frac{\hbar}{|e| B}\right)^{1/2}\]It is independent of the mass of the particle and depends only on the magnetic field strength:
1 T: \(l_B= 25.6556\) nm
2 T: \(l_B= 18.1413\) nm
3 T: \(l_B= 14.8123\) nm
In the above formula, \(\omega_c\) is the cyclotron frequency:
\[\omega_c = \frac{|e| B}{m_e^*}\]Thus for the electrons in GaAs, where \(m_e^*=0.067m_0\), it holds for the different magnetic field strengths:
1 T: \(\hbar\omega_c = 1.7279\) meV
2 T: \(\hbar\omega_c = 3.4558\) meV
3 T: \(\hbar\omega_c = 5.1836\) meV
Results¶
The calculated energy spectra for different magnetic fields (1 T, 2 T, 3 T) are as follows:
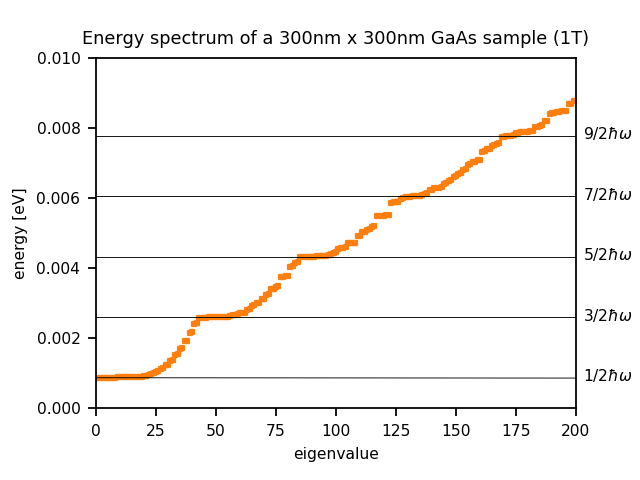
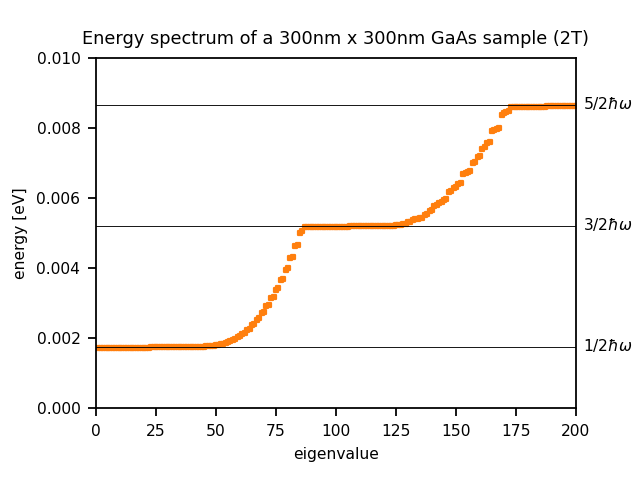
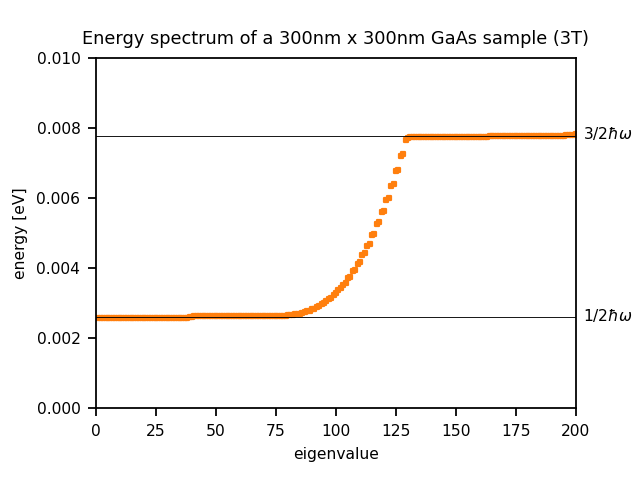
Landau levels
The Landau levels are analytically given by
where \(n = 1,2,3,...\)
The number of states for each Landau level can be calculated as follows (see P.Y. Yu, M. Cardona, Fundamentals of Semiconductors, p. 536, 3rd ed.):
where \(L_x\) and \(L_y\) are the lengths in the x and y directions (300 nm in this example) and \(l_B\) is the magnetic length. Here we ignore spin.
\(N\)(1 T) = 21.76 ~ 22 states per Landau level (in the figure above: 42)
\(N\)(2 T) = 43.52 ~ 44 states per Landau level (in the figure above: 86)
\(N\)(3 T) = 65.29 ~ 65 states per Landau level (in the figure above: 130)
When magnetic_field{} is specified, nextnano++ caculates the Schrödinger-Pauli equation, which takes into account the spin. Since the interaction energy between the spin and magnetic field is small compared to the separation of Landau levels, the number of states per Landau level calculated by nextnano++ is almost double of the analytical result that ignores the spin.
Energy eigenvalues
For the calculations, we used the symmetric gauge \(A = - \frac{1}{2} r \times B = \frac{1}{2} B \times r\) leading to the following energies (see J.H. Davies, The Physics of Low-Dimensional Semiconductors, p. 222):
One can see that all states having a negative value of \(l\) are degenerate with the states with \(l=0\), i.e. the allowed energies are independent of \(l\) if \(l<0\) (for the same \(n\)). The energies increase if \(l\) increases (for \(l>0\) and for the same \(n\)).
Last update: nn/nn/nnnn