Strain effects in freestanding nitride nanostructures¶
Attention
This tutorial is under construction
- Input files:
Strained-QW_AlGaN-GaN_Povolotskyi_PSS_2005_3D_nnp.in
- Scope:
This tutorial aims to simulate strain effects in a lattice mismatched, freestanding heterostructure with wurtzite crystal structure consisting of an AlGaN/GaN quantum well. This tutorial is based on [Povolotskyi2005].
- Output files:
Strain/strain_simulation_2d_slice_middle_along_yz.vtr
Strain/hydrostatic_strain_2d_slice_middle_along_yz.vtr
Strain/strain_simulation_2d_slice_boundary_along_xz.vtr
Strain/elastic_energy_density_2d_slice_middle_along_yz.vtr
Structure¶
Figure 2.5.1.76 shows the AlGaN/GaN/AlGaN quantum well structure, which is simulated in this tutorial. A 4 nm wide GaN QW layer is embedded between two \(\mathrm{Al_{0.28}Ga_{0.72}N}\) layers. The bottom AlGaN layer has a width of 10 nm, whereas the top AlGaN layer has a width of 6 nm. The overall shape of this nitride nanowire structure has the form of a cuboid with 50 nm x 50 nm extensions in the \(x\)- and \(y\)-directions. The height in the \(z\)-direction is 20 nm. The overall structure is surrounded by air (i.e. with a material where all elastic constants are zero).
The calculated strain pattern of this AlGaN/GaN structure is found to be highly non-homogeneous. The elastic energy has been minimized using continuum elasticity theory. We assume that the external stress applied to the structure is zero (freestanding structure).

Figure 2.5.1.76 Simulated heterostructure consisting of a GaN (green) layer sandwiched in between two AlGaN (blue) layers.¶
Results¶
Strain tensor components¶
In this section we show several strain tensor components \(\epsilon_{ij}(x, y, z)\) as a function of position \((x, y, z)\) for slices through the structure (vertical cross-section of the structure). Note that GaN has a larger lattice constant than AlGaN. Consequently, we expect the GaN layer to be compressively strained and the AlGaN layers to be tensely strained (or rather unstrained).
Figure 2.5.1.77 shows the strain tensor component \(\epsilon_{xx}\) along \(y\), \(z\) at \(x = 25.0\,\mathrm{nm}\). The corresponding data can be found in the file Strain/strain_simulation_2d_slice_middle_along_yz.vtr. The bottom AlGaN layer is rather unstrained (at the bottom), the GaN QW layer is strained compressively along the \(x\)-direction (blue region). This is not a surprise as we assumed coherent interfaces, i.e. the atomic planes match each other perfectly (pseudomorphic strain). The GaN QW induces a tensile strain to the AlGaN top layer (red region).
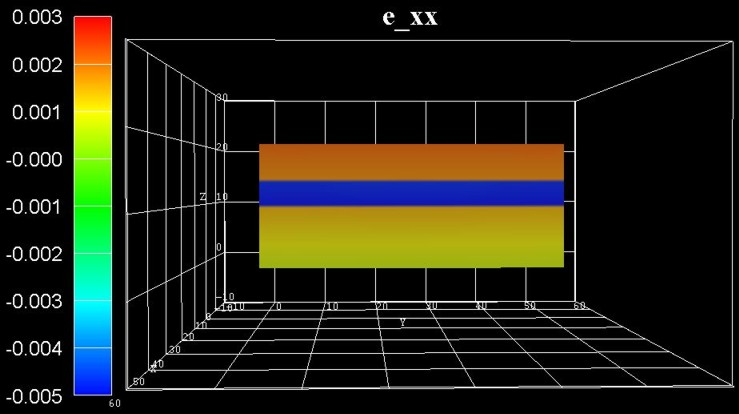
Figure 2.5.1.77 Calculated strain component \(\epsilon_{xx}\) in the \(y\), \(z\) plane at \(x = 25.0\,\mathrm{nm}\).¶
Figure 2.5.1.78 shows the strain tensor component \(\epsilon_{yy}\). Similar to Figure 2.5.1.77, the GaN layer is compressively strained (blue region), but only in the center and not at the boundaries, where it is nearly relaxed. Note that the \(\epsilon_{xx}\) and \(\epsilon_{yy}\) strain tensor components are not symmetric. This is due to the nitride crystal structure which has hexagonal symmetry perpendicular to the \((x, y)\) plane (and not cubic symmetry as the geometry of the structure).
In the center (blue region), the GaN takes on the lattice constant of AlGaN (compressive strain).
At the QW boundaries, the GaN takes on the lattice constant of ~GaN (nearly fully relaxed).
Below and above the QW boundaries (red regions), the AlGaN takes on the lattice constant of ~GaN (tensile strain).
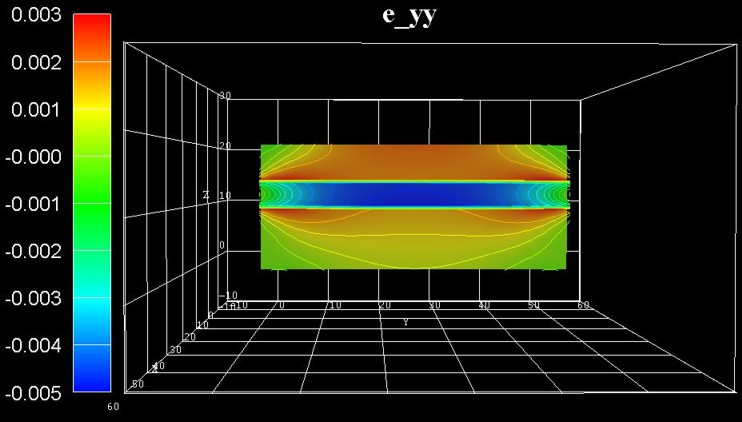
Figure 2.5.1.78 Calculated strain component \(\epsilon_{yy}\) in the \(y\), \(z\) plane at \(x = 25.0\,\mathrm{nm}\).¶
Figure 2.5.1.79 shows the strain tensor component \(\epsilon_{zz}\). As the GaN layer is compressively strained along both the \(x\)- and \(y\)-directions, it is tensilely strained (green region) along the \(z\)-direction (biaxially strained GaN layer, Poisson ratio).
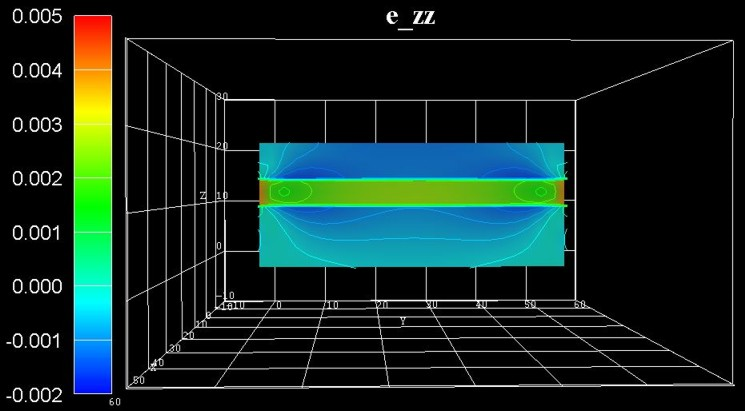
Figure 2.5.1.79 Calculated strain component \(\epsilon_{zz}\) in the \(y\), \(z\) plane at \(x = 25.0\,\mathrm{nm}\).¶
Figure 2.5.1.80 shows the hydrostatic strain \(\epsilon_\mathrm{hydro} = \epsilon_{xx} + \epsilon_{yy} + \epsilon_{zz}\), which is the trace of the strain tensor, i.e. the sum of the diagonal strain tensor components. It corresponds to the overall volume change. The data can be found in the file Strain/hydrostatic_strain_2d_slice_middle_along_yz.vtr. The blue region indicates that the GaN is strained compressively. AlGaN is mostly unstrained apart from the red regions at the left and right boundaries of the material interfaces. In a real sample, due to the deformation, the heterostructure changes its shape and becomes bent. In our case, the strain is small (less than \(1\%\)), so the shape of the structure does not change significantly.
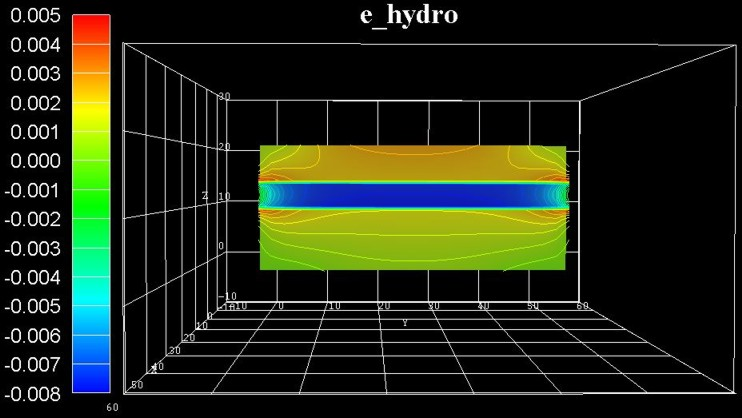
Figure 2.5.1.80 Calculated hydrostatic strain component \(\epsilon_\mathrm{hydro} = \epsilon_{xx} + \epsilon_{yy} + \epsilon_{zz}\) in the \(y\), \(z\) plane at \(x = 25.0\,\mathrm{nm}\).¶
In contrast to heterostructures, which are infinitely large and homogeneous in the lateral directions (i.e. in the \((x,y)\) plane), the deformation of a structure of a finite size is not homogeneous, as e.g. in GaN nanowire heterostructures. Since the structure is grown along the high symmetry direction [0001], the strain patterns exhibits reflection symmetry along the axis through the center (oriented parallel to the \(z\)-axis). The deformation becomes homogeneous in the region near the central axis, reproducing the case of an infinitely large structure.
Figure 2.5.1.81 shows the off-diagonal strain tensor component \(\epsilon_{yz}\). The strain tensor components \(\epsilon_{xy}\) and \(\epsilon_{xz}\) are zero for this particular slice. (In fact, the maximum value of \(\epsilon_{xy}\) is an order of magnitude smaller that the maximum value of \(\epsilon_{xz}\) or \(\epsilon_{yz}\).)
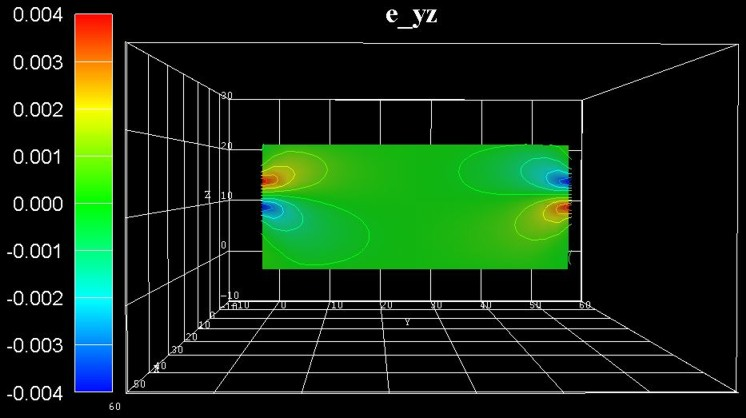
Figure 2.5.1.81 Calculated strain component \(\epsilon_{yz}\) in the \(y\), \(z\) plane at \(x = 25.0\,\mathrm{nm}\).¶
Figure 2.5.1.82 shows the same off-diagonal strain tensor component \(\epsilon_{yz}\), but this time at slices at the left and right boundaries. The corresponding data can be found in the file Strain/strain_simulation_2d_slice_boundary_along_xz.vtr
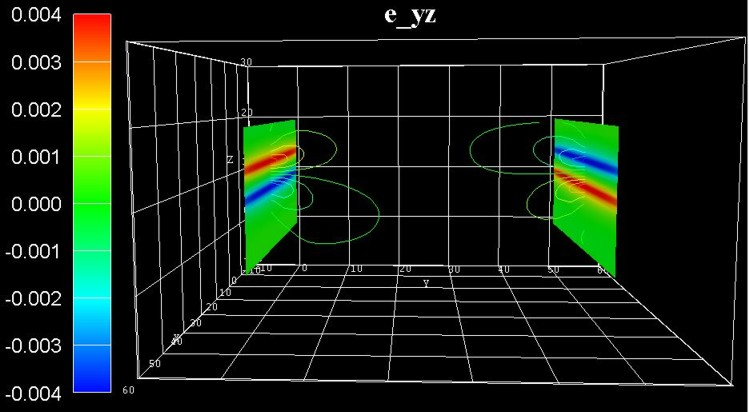
Figure 2.5.1.82 Calculated strain component \(\epsilon_{yz}\) in the \(x\), \(z\) plane at the boundaries.¶
Elastic energy density¶
Due to a possible usage of such structures as a light emitter, the strain in the GaN layer where charge carriers are confined, is or particular interest, i.e. the influence of stain on the conduction and valence band structure through deformation potentials. Additional, piezoelectric and pyroelectric fields have to be taken into account. The piezoelectric fields depend on the strain distribution in the sample. Thus, both the piezoelectric field and the GaN energy gap will vary along the lateral direction.
Figure 2.5.1.83 shows the energy density of the elastic deformation in units of \([\mathrm{eV/nm^3}]\). The corresponding data can be found in the file Strain/elastic_energy_density_2d_slice_middle_along_yz.vtr. The accumulated elastic energy in the pseudomorphically grown GaN QW is gradually reduced towards the free surface along the lateral direction. Consequently, the GaN QW center is almost fully strained, whereas towards the lateral surface there is a continuous relaxation.
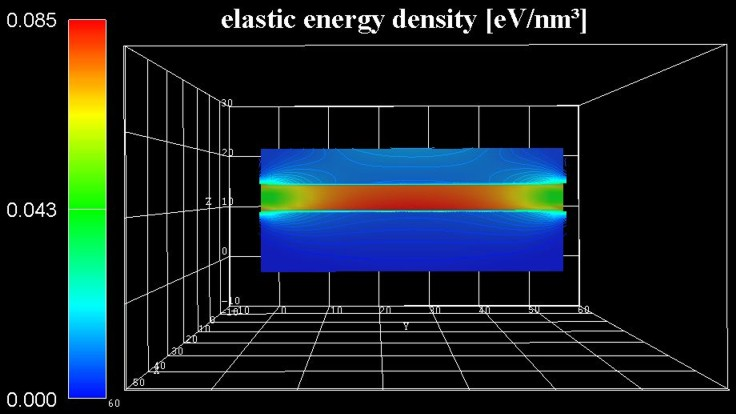
Figure 2.5.1.83 Elastic energy density in the \(x\), \(z\) plane at \(x = 25.0\,\mathrm{nm}\).¶
Last update: nn/nn/nnnn