I–V characteristics of n-doped Si structure

Attention

This tutorial is under construction

Input files:

• I-V_n-doped-Si_1D_nnp.in

• I-V_n-doped-Si_2D_nnp.in

• I-V_n-doped-Si_3D_nnp.in

• I-V_nin-doped-Si_1D_nnp.in

• I-V_nin-doped-Si_2D_nnp.in

• I-V_nin-doped-Si_3D_nnp.in

Scope:

This tutorial aims to simulate the I-V characteristics of n-doped and n-i-n doped Si structures.

Output files:

• IV_characteristics.dat

• bias_xxxxx/bandedges.dat

I-V characteristics of an n-doped Si structure

Structure

The structure we are dealing with consists of bulk Si that is sandwiched between two contacts. The whole structure has the following dimensions (see also):

• along \(x\)-axis: \(20\,\mathrm{nm}\) (\(1\,\mathrm{nm}\) contact, \(18\,\mathrm{nm}\) Si, \(1\,\mathrm{nm}\) contact)

• along \(y\)-axis: \(5\,\mathrm{nm}\)

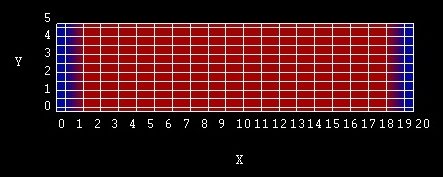
Figure 2.5.1.52 Simulated structure consisting of a left and right contact (blue) and n-doped Si layer (red).

The Si is n-type doped with a donor concentration of \(N_\mathrm{D} = 1\cdot 10^{20}\,\mathrm{cm^{-3}}\). The energy level is 0.044 eV below the conduction band edge. This leads to an electron density of \(n = 13.48 \cdot 10^{18}\,\mathrm{cm^{-3}}\), which corresponds to the concentration of the ionized donors. The Fermi level \(E_\mathrm{F}\) is taken to be at 0 eV in an equilibrium simulation, i.e. \(V = 0\,\mathrm{V}\). The distance of the conduction band from the Fermi level can be calculated in the following way:

• For the effective electron mass at the \(\Delta\)-point we have:

\[m_e = m^*_{e,\mathrm{DOS}} = (m_\mathrm{l}\cdot m_\mathrm{t}\cdot m_\mathrm{t})^{\frac{1}{3}} = (0.916\cdot 0.19^2)^{\frac{1}{3}} m_0 = 0.321 m_0,\]

where \(m_\mathrm{l}\) is the longitudinal and \(m_\mathrm{t}\) is the transversal mass of the effective mass tensor.

• The effective density of states reads:

\[N_\mathrm{c} = 12\cdot \left(\frac{2 \pi m_e k_\mathrm{B}T}{h^2}\right)^{\frac{3}{2}} = 12\cdot (0.321 \cdot 0.026 \cdot 2.0886\cdot 10^{14})^{\frac{3}{2}} = 12 \cdot 2.282\cdot 10^{18}\,\mathrm{cm^{-3}} = 2.738\cdot 10^{19}\,\mathrm{cm^{-3}},\]

where the factor of 12 arises due to the six-fold degeneracy of Si at \(\Delta\) and the two-fold spin degeneracy. Similarly, we obtain the effective density of states for holes:

\[ \begin{align}\begin{aligned}\begin{aligned}\\N_{\mathrm{v,\, hh}} &= 9.875\cdot 10^{18}\,\mathrm{cm^{-3}},\\N_{\mathrm{v,\, lh}} &= 1.502\cdot 10^{18}\,\mathrm{cm^{-3}}.\\\end{aligned}\end{aligned}\end{align} \]

Note that heavy and light holes are degenerate for \(k = 0\), i.e. \(N_\mathrm{v} = N_\mathrm{v,\,hh} + N_\mathrm{v,\,lh} = 1.1377\cdot 10^{19}\,\mathrm{cm^{-3}}\).

• The Semiconductor equation is given by

\[np = n_\mathrm{i}^2 = N_\mathrm{c} N_\mathrm{v} \exp\left( - \frac{E_\mathrm{gap}}{k_\mathrm{B}T}\right) = N_\mathrm{c}\cdot 1.138\cdot 10^{19}\,\mathrm{cm^{-3}}\exp\left(-\frac{1.095}{0.026}\right) = 1.238\cdot 10^{20}\,\mathrm{cm^{-6}},\]

with \(E_\mathrm{gap} = 1.095\,\mathrm{eV}\), \(n_\mathrm{i} = 1.113\cdot 10^{10}\mathrm{cm^{-3}}\) and \(p = n_\mathrm{i}^2/n = 9.185\,\mathrm{cm^{-3}}\).

• The occupation of the different energy states can either be described by Maxwell-Boltzmann statistics:

\[ \begin{align}\begin{aligned}\begin{aligned}\\n(T) &= N_\mathrm{c}(T)\exp\left(\frac{E_\mathrm{F} - E_\mathrm{c}}{k_\mathrm{B}T}\right),\\p(T) &= N_\mathrm{v}(T)\exp\left(\frac{E_\mathrm{v} - E_\mathrm{F}}{k_\mathrm{B}T}\right),\\\end{aligned}\end{aligned}\end{align} \]

or Fermi-Dirac statistics:

\[ \begin{align}\begin{aligned}\begin{aligned}\\ n(T) &= N_\mathrm{c}(T) \mathcal{F}_{1/2}\left(\frac{E_\mathrm{F} - E_\mathrm{c}}{k_\mathrm{B}T}\right),\\p(T) &= N_\mathrm{v}(T) \mathcal{F}_{1/2}\left(\frac{E_\mathrm{v} - E_\mathrm{F}}{k_\mathrm{B}T}\right),\\\end{aligned}\end{aligned}\end{align} \]

where \(\mathcal{F}_{1/2}\) is the Fermi-Dirac integral of order \(1/2\) multiplied by the factor \(2/\sqrt{\pi}\) (i.e. \(\mathcal{F}_{1/2}\) includes the Gamma pre-factor)

When using the Maxwell-Boltzmann statistics as an approximation, we obtain:

\[ \begin{align}\begin{aligned}\begin{aligned}\\E_\mathrm{c} &= k_\mathrm{B}T \ln\left(\frac{N_\mathrm{c}}{n}\right) = 0.026\,\mathrm{eV}\cdot\ln\left(\frac{2.738\cdot 10^{19}\,\mathrm{cm^{-3}}}{13.478\cdot 10^{18}\,\mathrm{cm^{-3}}}\right) = 0.026\,\mathrm{eV}\cdot \ln(2.031) = 18.3\,\mathrm{meV},\\E_\mathrm{v} &= - k_\mathrm{B}T \ln\left(\frac{N_\mathrm{v}}{p}\right) = - 0.026\,\mathrm{eV} \cdot 42.538 = - 1.099\,\mathrm{eV}.\\\end{aligned}\end{aligned}\end{align} \]

Note that nextnano++ uses the Fermi-Dirac integrals (Fermi-Dirac statistics), where the following results are obtained: \(E_\mathrm{c}=13.85\,\mathrm{meV}\) and \(E_\mathrm{v} = -1.0815\,\mathrm{eV}\).

Results

We sweep the voltage at the right contact from \(0.0\,\mathrm{V}\) to \(0.2\,\mathrm{V}\) in 10 steps. The input files used for the simulations are I-V_n-doped-Si_1D_nnp.in, I-V_n-doped-Si_2D_nnp.in I-V_n-doped-Si_3D_nnp.in. The calculated current density for each bias point can be found in IV_characteristics.dat. The resulting I-V characteristics is depicted in Figure 2.5.1.53.

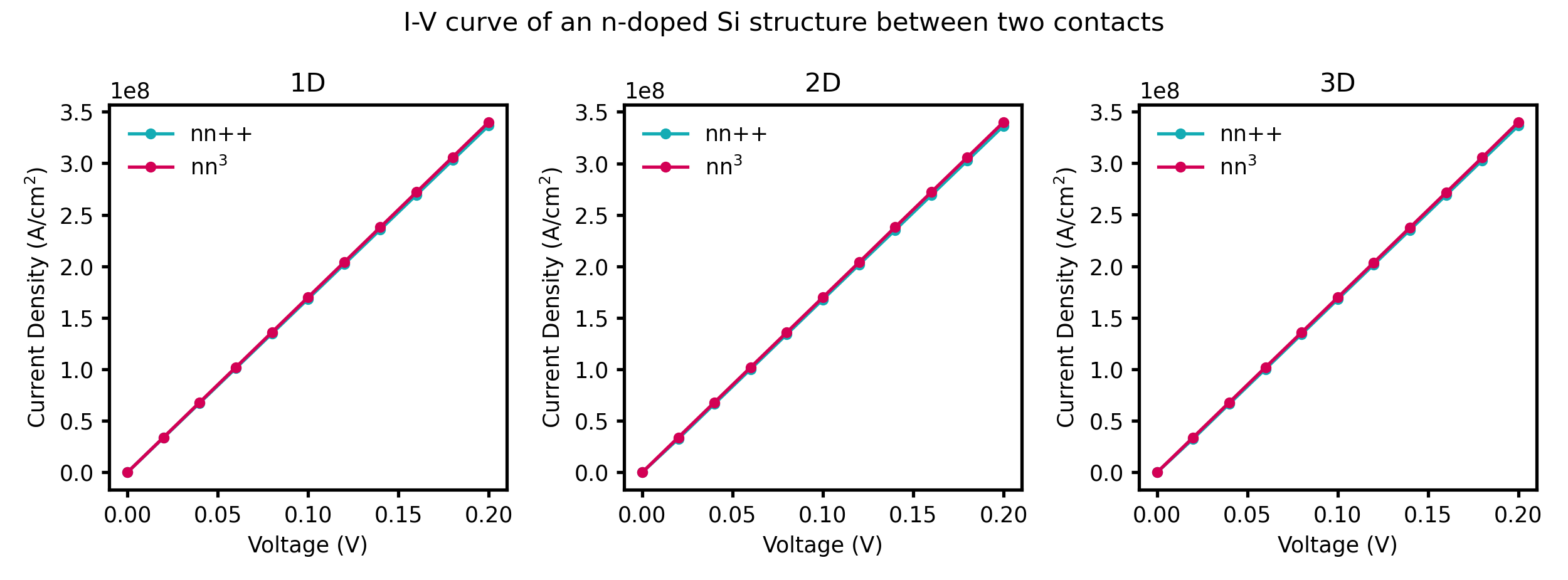
Figure 2.5.1.53 Simulated I-V characteristics of an n-doped Si structure using constant mobility model.

The nextnano++ results are in agreement with the I-V characteristics obtained with nextnano³. The units for the current in a 2D simulation are [\(\mathrm{A/m}\)]. Dividing this two-dimensional current value by the width of the device (in our case 5 nm) we obtain the current in units of [\(\mathrm{A/cm^2}\)], which is the usual unit of a 1D simulation. As our simple 2D example structure is basically equivalent to a 1D structure we can easily compare our 2D results with the 1D results to check for consistency. It is also possible to perform a 3D simulation. In this case, the units for the three-dimensional current are [\(\mathrm{A}\)]. Dividing by the area of the device of \(25\,\mathrm{nm^2}\), we obtain the 1D units of [\(\mathrm{A/cm^2}\)].

I-V characteristics of an n-i-n-doped Si structure

Structure

The second example is an n-i-n (n-doped, intrinsic, n-doped) Si structure, which is shown in Figure 2.5.1.54. The width of the intrinsic region is 14 nm, and the n-doped regions are both 2 nm wide.

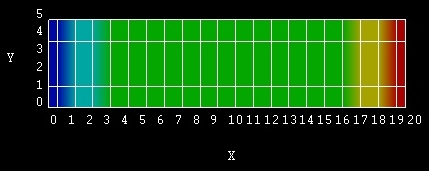
Figure 2.5.1.54 Simulated n-i-n structure consisting of a left contact (dark blue), n-doped Si (light blue), intrinsic Si (green), n-doped Si (yellow) and right contact (red).

Results

In Figure 2.5.1.55 the current-voltage (I-V) characteristic is shown. The input files used for the simulations are I-V_nin-doped-Si_1D_nnp.in, I-V_nin-doped-Si_2D_nnp.in I-V_nin-doped-Si_3D_nnp.in. The data of the I-V curve can be found in the corresponding file IV_characteristics.dat.

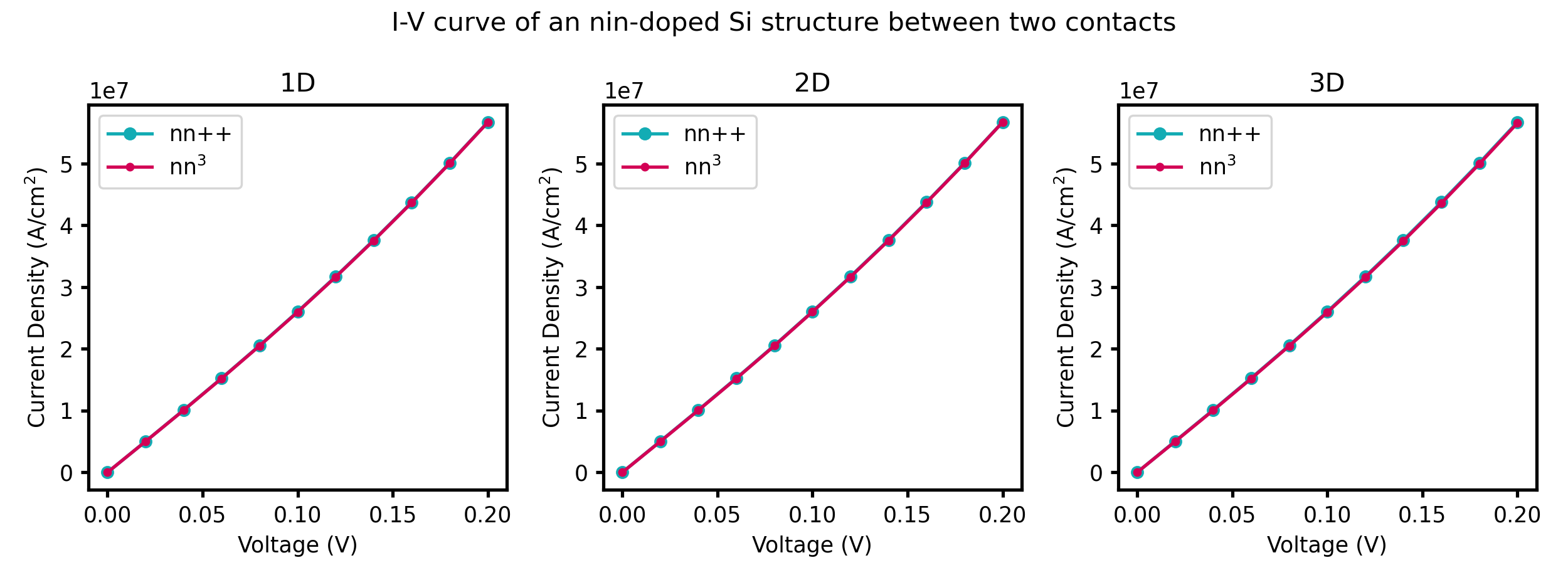
Figure 2.5.1.55 Simulated I-V characteristics of the n-i-n doped Si structure using constant mobility model.

In order to compare the results from 1D, 2D and 3D simulations, we have divided the 2D current by the width of the device (in our case 5 nm) and the 3D current by the cross-section area of the device of (in our case \(25\,\mathrm{nm^2}\)), to get the current density in units of [\(\mathrm{A/cm^2}\)]. The obtained results are in perfect agreement.

Figure 2.5.1.56 shows the conduction band profile (bias_xxxxx/bandedges.dat) for different voltages.

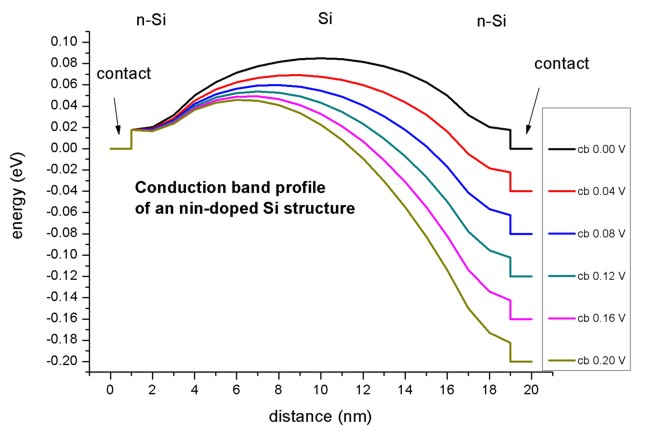
Figure 2.5.1.56 Simulated conduction band profile of the n-i-n Si structure for different voltages.

Last update: nn/nn/nnnn