4.8.6. Hexagonal GaN/AlN Quantum Dot

Conduction and valence band alignment in AlN/GaN QWs

In this section the input file QD_GaN_Andreev_PRB_2000_1D_nnp_band-offsets.in is used to compute band offsets without strain effects. The input file QD_GaN_Andreev_PRB_2000_1D_nnp_strain.in is used to show impact of the strain on the band edges without piezo effects.

Figure 4.8.6.1 shows the conduction and valence band edge alignment in AlN/GaN structures, strained and unstrained. In AlN, the light hole (LH) is the highest valence band whereas in GaN, this is the heavy hole (HH). We assumed a valence band offset of VBO = 0.5 eV, the conduction band offset is much larger (CBO = 2.3 eV). All material parameters are based on [Andreev2000] although meanwhile better parameters are available.

The lattice constants in GaN are larger than in AlN, thus GaN is compressively strained in the case of pseudomorphic growth on the AlN substrate. The AlN band edges are the same as in the unstrained calculation, only the GaN edges have changed:

  • The band gap of GaN has increased (compressive strain increases the band gap).

  • Now the crystal-field split-hole (CH) in GaN lies above the light hole (LH) and close to the heavy hole (HH).

  • The valence band offset has decreased to VBO = 0.46 eV.

  • The conduction band offset has decreased to CBO = 2.15 eV.

../_images/tutorials_QD_GaN_Andreev_PRB_2000_1D_3D_nopoisson.svg

Figure 4.8.6.1 Conduction band edge (CB) and valance band edges (HH, LH, CH) of the 1D AlN/ GaN QD: (a) unstrained; (b) pseudomorphic strain.

Conduction and valence band edges in AlN/GaN QWs (pseudomorphically strained, including piezo- and pyroelectric fields)

In this section the input file QD_GaN_Andreev_PRB_2000_1D_nnp_strain-PzPr-poisson-1b.in or QD_GaN_Andreev_PRB_2000_1D_nnp_strain-PzPr-poisson-6kp.in can be used to observe piezo effect on the design.

In Figure 4.8.6.2 the effect of piezo- and pyroelectric fields on the band edge is shown. The band edge gets tilted due to the additional electric potential arising from the piezo- and pyroelectric charges. The electrostatic potential which is the solution to the Poisson equation is also shown.

The electron and hole wavefunctions (\(\Psi^2\)) in a 5.1 nm AlN/GaN/AlN quantum well are shown as well. For the electrons, the single-band effective-mass approximation was used whereas for the holes the 6-band k.p model was used. The figure shows the four lowest electron eigenstates and the 6 highest valence band eigenstates. All eigenstates are two-fold degenerate due to spin.

../_images/tutorials_QD_GaN_Andreev_PRB_2000_1D_3D_wavefunctions1D.svg

Figure 4.8.6.2 5.1 mm AlN/GaN/AlN quantum well. (a) Conduction band edge (CB) and valance band edges (HH, LH, CH) of the 1D AlN/GaN QD (strained on AlN substrate) including piezo- and pyroelectric fields. (b) Electron and hole wavefunctions \(\Psi^2\) of a 5.1 mm AlN/GaN/AlN quantum well.

Hexagonal shaped GaN quantum dot embedded in AlN (wurtzite)

The simulated hexagonal GaN quantum dot (height = 4.1 nm) is embedded in an AlN matrix, input file QD_GaN_Andreev_PRB_2000_3D_nnp.in. The wetting layer is 1 nm thick and consists of GaN. The structure and a cross-section of the structure along x-y are shown in Figure 4.8.6.3.

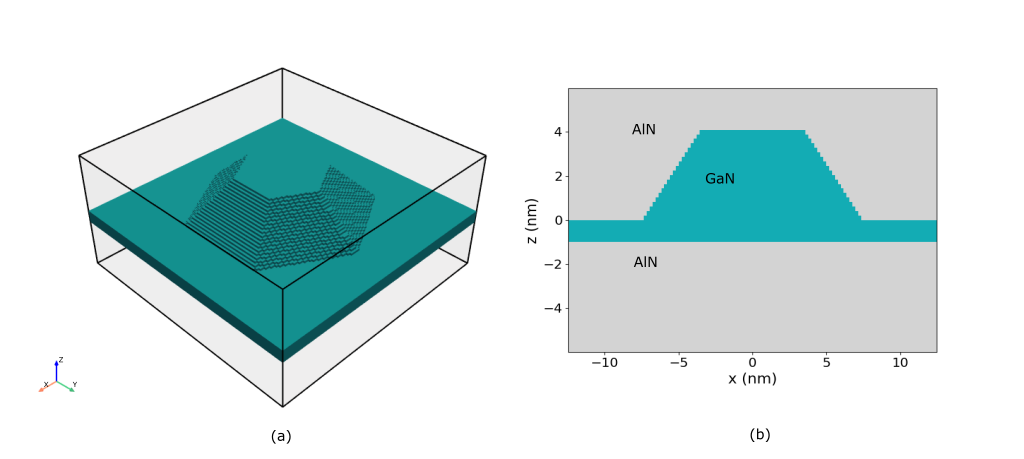
../_images/tutorials_QD_GaN_Andreev_PRB_2000_3D_material.png

Figure 4.8.6.3 3D AlN/GaN hexagonal quantum dot.

The strain tensor components of a different lines along the z- abd y-axis are shown in Figure 4.8.6.4. This figure is related to Fig. 2 in [Andreev2000].

../_images/tutorials_QD_GaN_Andreev_PRB_2000_3D_nnp_strain.svg

Figure 4.8.6.4 Strain tensor along the different lines in the hexagonal GaN quantum dot. (a) Along the z-axis through the center of the QD: (x, y) = (0, 0) nm. (b) Along the z-axis outside of QD: (x, y) = (12.75, 0) nm. (c) Along the y-axis through the bottom of the QD: (x, z) = (0, 0.1) nm. (d) Along the y-axis through the wetting layer: (x, z) = (0, -0.5) nm.

The strain induced piezoelectric fields and the pyroelectric fields lead to the electrostatic potential which is shown in Figure 4.8.6.5. The figures of the potential are related to Fig. 4 in [Andreev2000]. In Figure 4.8.6.5 (a) one can clearly see that the electrostatic potential has its maximum at the top of the QD and its minimum in the wetting layer area just below the QD. Figure 4.8.6.5 (b) shows a cut of the electrostatic potential through the wetting layer plane.

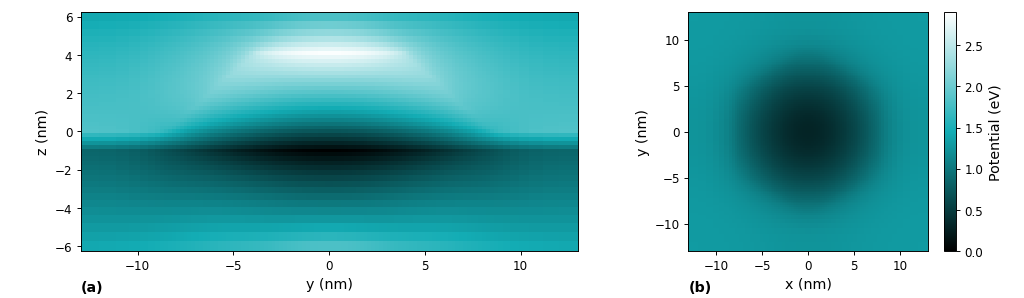
../_images/tutorials_QD_GaN_Andreev_PRB_2000_3D_potential.png

Figure 4.8.6.5 Electrostatic potential inside the quantum dot. (a) The slice at x = 0 nm; (b) cut through the wetting layer at y = 0 nm.

The conduction and valence band edges are shown in Figure 4.8.6.6. One can clearly see that the conduction band minimum is located in the top of the quantum dot whereas the maximum for the valence band is located inside the wetting layer (WL) (which is equivalent to the bottom of the quantum dot). Thus, one expects the electrons, which are located in the top area of the QD, to be spatially separated from the holes, which are located in the WL (bottom of the QD). The figures of the conduction and valence band edges are related to Figs. 5 and 6 in [Andreev2000].

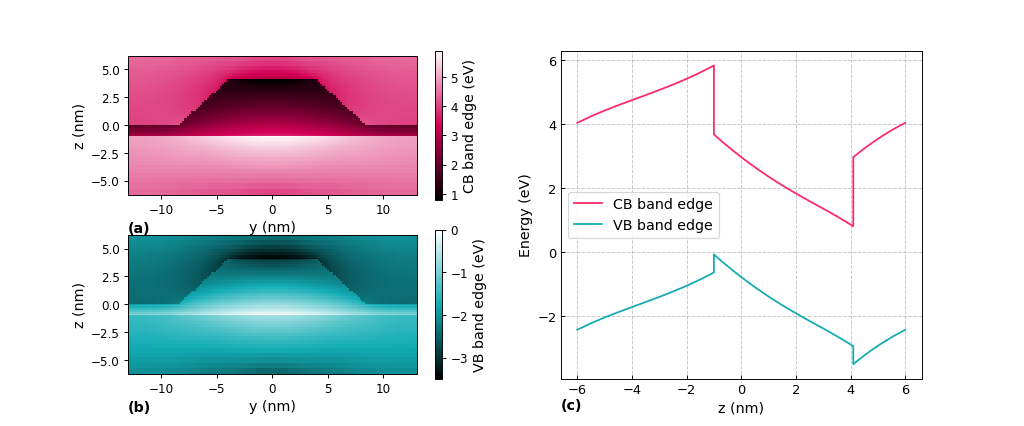
../_images/tutorials_QD_GaN_Andreev_PRB_2000_3D_bandedges.png

Figure 4.8.6.6 Conduction and valence band edges. (a) Conduction band edges at x = 0 nm. (b) Valence band edge of the QD at x = 0 nm. (c) Conduction and valence band edges of the QD at (x, y) = (0, 0) nm.

The electron states are located near the top of the quantum dot where the conduction band has a minimum.

The isosurfaces of the six lowest electron states of the quantum dot are shown in Figure 4.8.6.7. The \(2^\mathrm{nd}\) and \(3^\mathrm{rd}\) eigenstates are degenerate, as well as the \(4^\mathrm{th}\), \(5^\mathrm{th}\) and \(6^\mathrm{th}\). The figures of the wave functions are related to Fig. 7 in [Andreev2000].

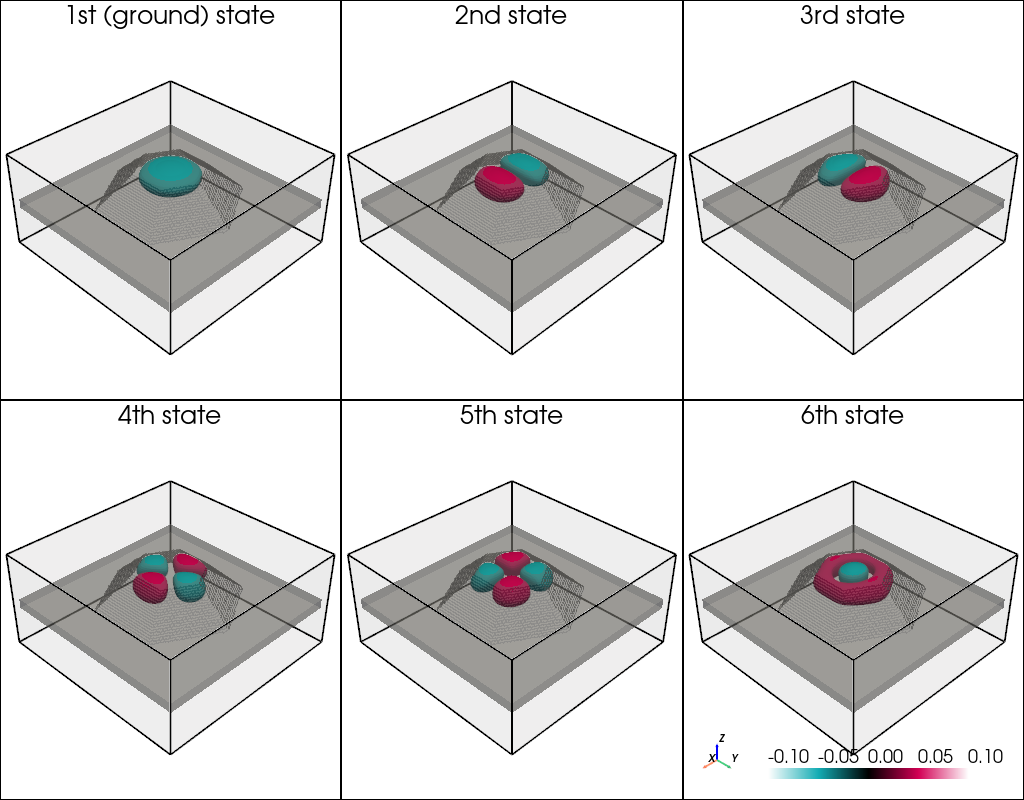
../_images/tutorials_QD_GaN_Andreev_PRB_2000_3D_wavefunctions.png

Figure 4.8.6.7 Electron states of the QD. The isosurfaces are set at values of \(\pm 0.05\). The gray volume indicates the GaN quantum dot and wetting layer.

This tutorial also exists for nextnano³.

Last update: 11/07/2024