|
| |
nextnano3 - Tutorial
next generation 3D nano device simulator
1D Tutorial
Parabolic Quantum Well (GaAs / AlAs)
Author:
Stefan Birner
If you want to obtain the input files that are used within this tutorial, please
check if you can find them in the installation directory.
If you cannot find them, please submit a
Support Ticket.
-> 1DGaAs_ParabolicQW.in
-> 1DGaAs_ParabolicQW_infinite.in
-> 1DGaAs_ParabolicQW_infinite_half.in
-> parabola_half-parabola_nn3.in / _nnp.in
Parabolic Quantum Well (GaAs / AlAs)
This tutorial aims to reproduce figures 3.11 and 3.12 (pp. 83-84) of
Paul Harrison's
excellent book "Quantum
Wells, Wires and Dots" (1st edition, Section 3.5 "The
parabolic quantum well"), thus the following description is based on the
explanations made therein.
We are grateful that the book comes along with a CD so that we were able to
look up the relevant material parameters and to check the results for
consistency.
General comments on the solutions of a parabolic potential
An ideal parabolic potential represents a "harmonic oscillator" which is
described in nearly every beginner's textbook on quantum mechanics.
The eigenstates can be calculated analytically and are given by the following
relationship:
En = ( n - 1/2 ) hbarw0
where n = 1, 2, 3, ...
One feature of a particle that is confined in such a well is that the energy
levels are equally spaced by hbarw0 above the zero point
energy of 1/2 hbarw0.
The eigenfunctions show an even-odd alternation which is also the case in
symmetric, square quantum wells.
The eigenenergies can be measured experimentally by analyzing the optical
transitions between the conduction and the valence band states, taking into
account the selection rules (both states must have the same parity, see tutorial
on interband transitions). For
intersubband transitions, different selection rules apply (see tutorial on
intersubband transitions). Such
an experiment can be used to measure the conduction and valence band offsets
because the curvature of the conduction and valence band edges (and thus the
eigenstates) depends on the offsets.
(More information on this can be found in The Physics of Low-Dimensional
Semiconductors - An Introduction, John H. Davies, Cambridge University Press
(1998).)
Parabolic quantum well: 10 nm AlAs / 10 nm AlGaAs / 10 nm AlAs
-> 1DGaAs_ParabolicQW.in
- It is possible to grow parabolic quantum wells by continuously varying the
composition of an alloy.
- Our structure consists of a 10 nm AlxGa1-xAs
parabolic quantum well (the x alloy content varies parabolically) that is surrounded by
10 nm AlAs barriers on each side.
We thus have the following layer sequence: 10 nm AlAs
/ 10 nm AlxGa1-xAs / 10 nm AlAs.
The barriers are printed in bold.
- This figure shows the conduction band edge and the three lowest electron
wave functions (psi) that are confined inside the parabolic quantum well.
All other states are not confined any more.
(Note that the energies were shifted so that the conduction band edge of GaAs
equals 0 eV.)
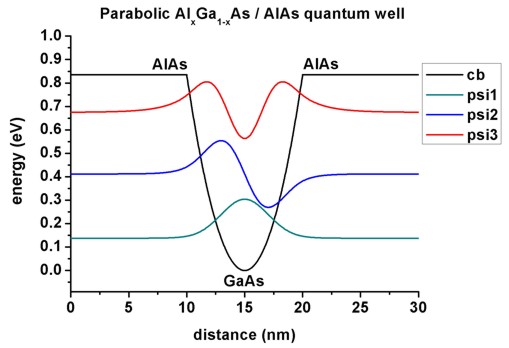
The figure is in perfect agreement with Fig. 3.11 (p. 83) of
Paul Harrison's
book "Quantum
Wells, Wires and Dots" (1st edition).
-
Technical details:
$material
...
material-number = 2
material-name =
Al(x)Ga(1-x)As !
cluster-numbers = 2
alloy-function =
parabolic
$end_material
$alloy-function
...
material-number = 2
function-name =
parabolic !
orientation =
0 0 1
!
vary-from-pos-to-pos = 10d0 20d0
!
xalloy-from-to =
0.0d0 1.0d0 !
$end_alloy-function
In agreement with Paul Harrison,
- we assumed a constant effective mass of 0.067 m0 throughout the
whole sample and
- assumed the conduction band offset between GaAs and AlAs to be 0.83549 eV.
- Output
a) The conduction band edge of the Gamma conduction band can be
found here:
band_structure / cb1D_001.dat
The 1st
column contains the position in units of [nm].
[eV].
Schroedinger_1band / cb001_qc001_sg001_deg001_dir_psi_squared_shift.dat
[nm].
Schroedinger_1band / cb001_qc001_sg001_deg001_dir_psi_shift.dat
[nm].
c)
This file contains the eigenenergies of the electron states. The units are [eV].
Schroedinger_1band / ev1D_cb001_qc001_sg001_deg001_dir.dat
but at the boundaries (i.e. from 0 nm to 5 nm and from 25
nm to 30 nm) we use a 0.1 nm grid to avoid long CPU times:
The eigenvalues read:
num_ev: eigenvalue [eV]:
1 0.1377775566
(0.10 / 0.05 / 0.02 / 0.05 / 0.10 nm grid)
2 0.4121053675
3 0.6754933822
1 0.1377754485
2 0.4121049460
3 0.6755000401
1
0.1377751623 (0.01
nm grid)
2 0.4121058503
3 0.6755025905
- 1/2 ) hbarw0
where n = 1, 2, 3, ... and w0 = (C/m*)1/2
(m* = effective mass, C = constant which is related to the parabolic potential
V(z) = 1/2 K z2 )
one can calculate hbarw0:
- 0 eV = 0.276 eV
- E1 = 0.274 eV
- E2 = 0.263 eV
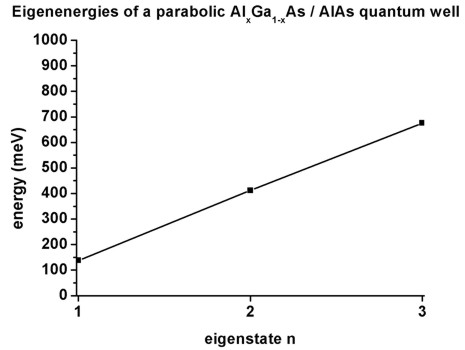
The figure is in perfect agreement with Fig. 3.12 (p. 84) of
Paul Harrison's
book "Quantum
Wells, Wires and Dots" (1st edition).
- Matrix elements
The following matrix elements have been calculated:
intraband-matrix-elements = o !
matrix element < psif* | psii >
This spatial overlap matrix elements simply returns the Kronecker
delta as expected because the wave functions are orthogonal.
==> Schroedinger_1band/intraband_o1D_cb001_qc001_sg001_deg001_dir.txt
intraband-matrix-elements = p !
matrix element < psif* | p | psii >
==> Schroedinger_1band/intraband_pz1D_cb001_qc001_sg001_deg001_dir.txt
intraband-matrix-elements = z ! dipole matrix
element < psif* | z | psii >
==> Schroedinger_1band/intraband_z1D_cb001_qc001_sg001_deg001_dir.txt
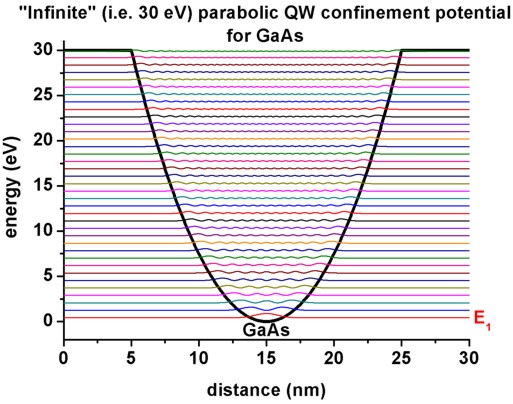
"Infinite" (30 eV) parabolic QW confinement for GaAs
-> 1DGaAs_ParabolicQW_infinite.in
- The following figure shows the eigenstates of a parabolic quantum well
(GaAs) where the confinement is assumed to be 30 eV.
Now up to 37 eigenstates are confined in the quantum well (grid resolution:
0.025 nm inside the well, 0.05 nm inside the barrier). The figure shows the
conduction band profile and the square of the wave functions (psin2)
for eigenstate n (n = 1, 2, ..., 37).
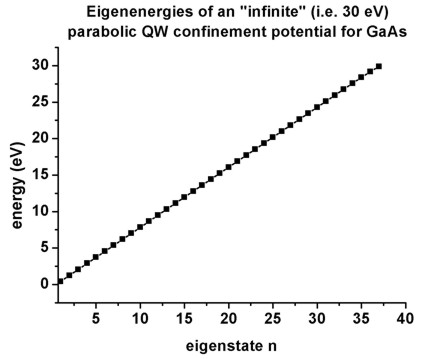
- This next figure shows the energies of the 37 confined electron states as
a funtion of eigenstate n.
As expected, the curve shows a linear dependence because the eigenstates are
equally spaced by
hbarw0 = 0.826 eV (where we used En
= ( n - 1/2 ) hbarw0).
- 0 eV = 0.8261 eV
E1 / (2 E1) = 0.5000
hbarw0 = E2
- E1 = 0.8260 eV
E2 / (2 E1) = 1.4999
hbarw0 = E3
- E2 = 0.8260 eV
E3 / (2 E1) = 2.4997
hbarw0 = E4
- E3 = 0.8259 eV
E4 / (2 E1) = 3.4994
hbarw0 = E5
- E4 = 0.8259 eV
E5 / (2 E1) = 4.4991
hbarw0 = E6
- E5 = 0.8258 eV
E6 / (2 E1) = 5.4987
hbarw0 = E7
- E6 = 0.8257 eV
E7 / (2 E1) = 6.4982
hbarw0 = E8
- E7 = 0.8257 eV
E8 / (2 E1) = 7.4978
Still, due to the "infinite" barrier of 30 eV (which is still a
finite barrier) that we have employed, the higher lying states deviate
slightly from the analytical results where infinite barriers have been
assumed. Thus a much higher barrier sho.
- One should bare in mind that the energy level spacing of such parabolic
quantum wells is inversely proportional to both the well width and the square
root of the effective mass.
- It is also interesting to look at the intraband matrix elements, i.e. to
investigate the probability for
intersubband transitions.
The relevant output is contained in these two files:
- Schroedinger_1band / intraband_pz1D_cb001_qc001_sg001_deg001_dir.txt -
pz
- Schroedinger_1band / intraband_z1D_cb001_qc001_sg001_deg001_dir.txt -
From the calculated oscillator
strengths it can be seen that only transitions from one level to the
neighboring levels (+1 and -1) are allowed.
Because in the case of a harmonic oscillator the momentum operator is
proportional to the sum of the creation and the annihilation operators, thus
only states can couple that have different occupation numbers with the
difference equal to 1.
"Infinite" (30 eV) half-parabolic QW confinement for GaAs
(Thanks to Michael Povolotskyi who suggested this half-parabolic structure!)
-> 1DGaAs_ParabolicQW_infinite_half.in
- The following figure shows the eigenstates when taking only the right half
of the parabolic quantum well
(GaAs) that has been calculated above. The confinement is 30 eV on the right
and infinite confinement on the left (Dirichlet boundary conditions).
Now only 18 eigenstates are confined in the quantum well, i.e. half the number
of the eigenvalues compared with the full parabolic QW (grid resolution:
0.025 nm inside the well, 0.05 nm inside the barrier). The figure shows the
conduction band profile and the square of the wave functions (psin2)
for eigenstate n (n = 1, 2, ..., 18).
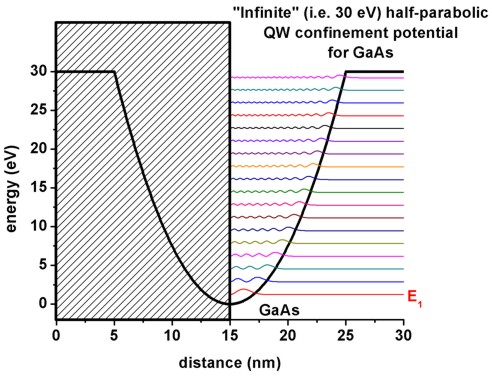
- Again, the eigenstates are
equally spaced. However, the separation energy is now twice the one as before:
hbarw0 = 2 * 0.826 eV = 1.65.
E1
= ( 3/2 ) hbarw0 / 2.
- E1 = 1.647 eV
- E2 = 1.648 eV
- E3 = 1.648 eV
- It is also interesting to look at the intraband matrix elements, i.e. to
investigate the probability for
intersubband transitions.
The relevant output is contained in these two files:
- Schroedinger_1band / intraband_pz1D_cb001_qc001_sg001_deg001_dir.txt -
pz
- Schroedinger_1band / intraband_z1D_cb001_qc001_sg001_deg001_dir.txt -
- We note that also more realistic parabolic quantum wells can be calculated
with nextnano≥.
Assuming that the alloy profile is parabolic,
- strain can be included (the strain tensor depends on the alloy
profile),
- as well as effective masses that depend on the alloy profile,
- an 8-band k.p model (necessary to get correct
intersubband transition energies)
- and bowing parameters (especially important for AlGaAs).
All these features are automatically included in the nextnano≥ code.
|