nextnano3 - Tutorial
next generation 3D nano device simulator
1D Tutorial
Optical interband transitions in a quantum well - Matrix elements and selection rules
Author:
Stefan Birner
-> 1DQW_interband_matrixelements_finite_nn3.in
/ *nnp.in - input file for the nextnano3 and nextnano++ software
-> 1DQW_interband_matrixelements_infinite_nn3.in /
*nnp.in -
-> 1DQW_interband_matrixelements_finite_kp_nn3.in
-> 1DQW_interband_matrixelements_infinite_kp_nn3.in
These input files are included in the latest version.
Optical interband transitions in a 5 nm AlAs / GaAs / AlAs quantum well - Matrix elements and selection rules
(Note: This tutorial has to be updated: Now we output the
square (!) of the matrix
element < psi_hl_i | psi_el_j >, i.e.
< psi_hl_i | psi_el_j >^2.)
Eigenstates and wave functions in the quantum well
- We consider a 5 nm GaAs quantum well embedded between AlAs barriers. The structure
is assumed to be unstrained.
We distinguish between two cases:
a) finite AlAs barriers
b) infinite "AlAs" barriers (This can be achieved by choosing Dirichlet
boundary conditions at the quantum well boundaries.)
- Case a):
-> 1DQW_interband_matrixelements_finite_nn3.in
For finite barriers we obtain using single-band Schrödinger
effective-mass approximation (i.e. isotropic and parabolic effective masses)
- 3 confined electron states in the Gamma conduction band (we don't
consider L and X bands here)
- 5 confined heavy hole states
- 2 confined light hole states
- 3 confined split-off hole states
The figure below shows the band edges of the Gamma
conduction band and the heavy,
light and split-off hole band edges together
with wave functions of the confined states. Note that the heavy and light hole band edge is
degenerate.
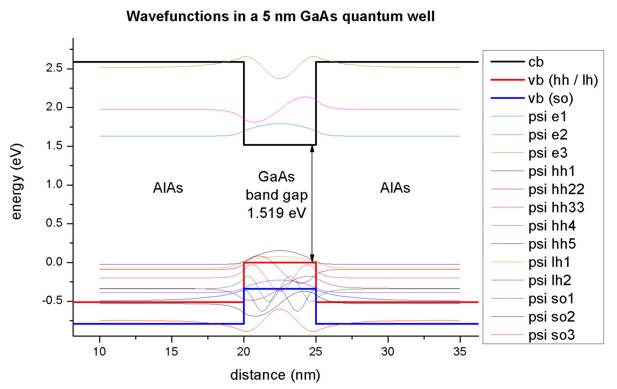
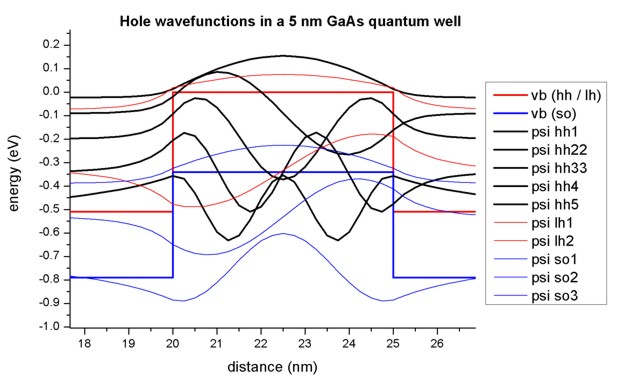
- As one can see the valence band looks rather messy. Thus we zoom into
it...
The 5 heavy hole wave functions are indicated in black, the 2 light hole
wave function in red and the 3 split-off
hole wave functions in blue.
- Case b) Infinite AlAs barriers
-> 1DQW_interband_matrixelements_infinite_nn3.in
To understand the optical transitions we first examine the matrix elements of
the envelope functions, i.e. the spatial overlap which is the integral over
their product with no dependence on polarization.
integral (psicn* (z) psivm
(z) dz)
In our case, we have a symmetric quantum well, thus our envelope functions are
either symmetric or antisymmetric. Therefore the matrix element
will vanish unless the envelope functions have the same parity.
Now let's simulate the same structure as above but this time we assume
infinite AlAs barriers:
Case b) -> 1DQW_interband_matrixelements_infinite.in
In this case, the two sets of envelope functions are the same for both
electron and hole wave functions and the integral becomes the Kronecker delta:
integral (psicn* (z)
psivm (z) dz) = deltanm
This leads to the so-called 'Delta n = 0' selection rule, i.e. only
transitions between levels with the same index are allowed. Of course, this
rule is not valid any more for case a) where we have finite AlAs barriers but
nevertheless this rule gives the strongest transitions.
$output-1-band-schroedinger
...
interband-matrix-elements = yes
complex-wave-functions =
yes ! to print out psi in addition to psi²
The spatial overlap integrals of the envelope functions are contained in these
files:
Schroedinger_1band/interband1D_vb001_cb001_qc001_hlsg001_deg001_dir.dat
- heavy hole
Schroedinger_1band/interband1D_vb002_cb001_qc001_hlsg002_deg001_dir.dat
-
Schroedinger_1band/interband1D_vb003_cb001_qc001_hlsg003_deg001_dir.dat
-
For instance, the matrix elements of the envelope functions for the 'heavy
hole' to 'conduction band' transitions read:
Spatial overlap matrix elements < psi_hl_i | psi_el_j > and
energy of transition in [eV].
heavy hole <-> Gamma conduction band
--------------------------------------------------------
<psi_vb001|psi_cb001> 1.001844
1.729371 ('Delta n = 0' selection rule)
<psi_vb001|psi_cb002> 3.456436E-016
<psi_vb001|psi_cb003> 7.866970E-016
<psi_vb002|psi_cb001> 7.463647E-016
<psi_vb002|psi_cb002> 1.007268
2.355209
<psi_vb002|psi_cb003> 2.844946E-016
<psi_vb003|psi_cb001> 9.575673E-016
<psi_vb003|psi_cb002> 1.450228E-015
<psi_vb003|psi_cb003> 1.015938 3.384106
<psi_vb004|psi_cb001> 1.076395E-015
<psi_vb004|psi_cb002> 1.422473E-015
<psi_vb004|psi_cb003> 2.019218E-015
<psi_vb005|psi_cb001> 1.960237E-016
<psi_vb005|psi_cb002> 1.346145E-015
<psi_vb005|psi_cb003> 1.217775E-015
For a 0.1 nm gridding one obtains the following values for the relevant
transitions:
<psi_vb001|psi_cb001>
1.000140
1.754633
<psi_vb002|psi_cb002> 1.000559
2.459675
<psi_vb003|psi_cb003> 1.001251
3.631886
- Case a) Finite AlAs barriers
We now calculate the same matrix elements as above but this time for the
finite AlAs barriers.
Spatial overlap matrix elements < psi_hl_i | psi_el_j > and
energy of transition in [eV].
heavy hole <-> Gamma conduction band
-------------------------------------
<psi_vb001|psi_cb001> 0.987507
1.654103 ('Delta n = 0' selection rule)
<psi_vb001|psi_cb002> 1.336279E-014
<psi_vb001|psi_cb003> 0.145559
2.538366
<psi_vb002|psi_cb001> 1.133344E-014
<psi_vb002|psi_cb002> 0.964789
2.065139
<psi_vb002|psi_cb003> 7.879180E-015
<psi_vb003|psi_cb001> 0.128041
1.829856
<psi_vb003|psi_cb002> 4.286800E-015
<psi_vb003|psi_cb003> 0.839306
2.714118
<psi_vb004|psi_cb001> 6.263441E-015
<psi_vb004|psi_cb002> 0.215428
2.315853
<psi_vb004|psi_cb003> 1.246759E-015
The results shown above are for a 0.25 nm grid spacing (which is rather
coarse).
For a 0.1 nm gridding one obtains the following values for the relevant
transitions:
<psi_vb001|psi_cb001> 0.987955
1.652509
<psi_vb001|psi_cb003>
0.142978
2.541682
<psi_vb002|psi_cb002> 0.966524
2.062825
<psi_vb003|psi_cb001>
0.127100
1.828683
<psi_vb003|psi_cb003> 0.838394
2.717855
<psi_vb004|psi_cb002>
0.211786
2.317309
6-band k.p calculations for the infinite barrier GaAs quantum well
-> 1DQW_interband_matrixelements_infinite_kp_nn3.in
The following figure shows the lowest 26 eigenstates obtained with 6-band k.p
for the 5 nm GaAs quantum well with infinite barriers. Each k.p state is
two-fold degenerate (spin up / spin down).
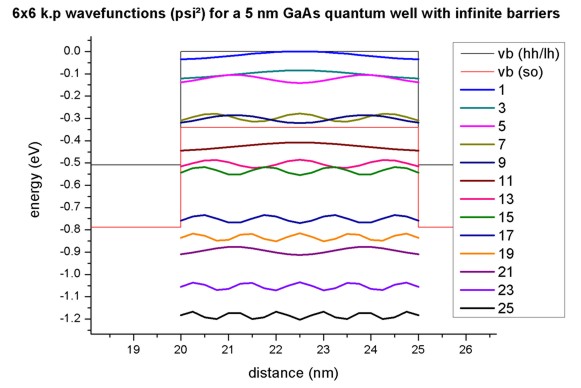
One can easily relate the transitions to the 'Delta n = 0' selection rule.
However, in contrast to the single-band approximation, the matrix elements are
not necessarily equal to 1 any more because the hole states are mixed and thus
the hole envelope functions are significantly different to the electron envelope
functions, even for an infinitely deep square well.
Spatial overlap matrix elements < psi_hl_i | psi_el_j >
and
energy of transition in [eV].
6-band k.p holes <-> Gamma conduction band
--------------------------------------------------------
...
6-band k.p calculations for the finite barrier AlAs/GaAs/AlAs quantum well
-> 1DQW_interband_matrixelements_finite_kp_nn3.in
- The following figure shows the 6-band k.p hole wave functions for the
quantum well having finite AlAs barriers. Their energies and psi² are two-fold
degenerate due to spin but the wave functions psi are different! (not shown
here)
The electron wave functions (3 confined states) are the same as above.
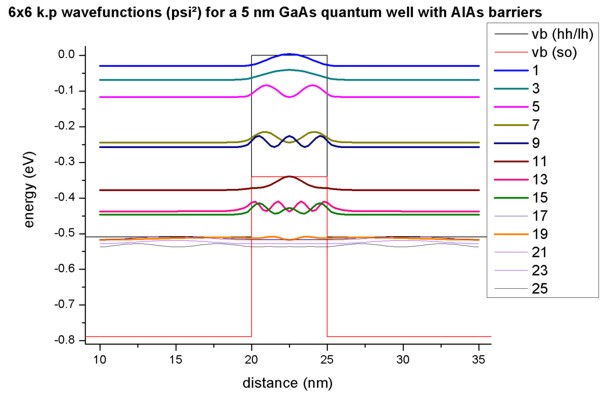
- The file
Schroedinger_kp/interband1D_vb001_cb001_qc001_hlsg001_deg001_dir.dat contains
the following spatial overlap integrals.
One can nicely see that in addition to the transitions where the 'Delta n = 0'
selection rule is responsible, additional transitions arise due to
symmetric/antisymmetric parity. All other transitions are zero. This is in
agreement with the single-band results.
Electric field in z-direction [kV/cm]: 0.000000000000000E+000
Spatial overlap matrix elements < psi_hl_i | psi_el_j > and
energy of transition in [eV].
6-band k.p holes <-> Gamma conduction band
--------------------------------------------------------
...
|