nextnano3 - Tutorial
next generation 3D nano device simulator
3D Tutorial
3D nanocrystals (spherical quantum dots)
Author:
Stefan Birner
If you want to obtain the input files that are used within this tutorial, please
check if you can find them in the installation directory.
If you cannot find them, please submit a
Support Ticket.
-> 3DsphericGaAsQD_exciton_01nm.in -
spherical QD with a diameter of 1 nm
-> 3DsphericGaAsQD_exciton_015nm.in -
-> 3DsphericGaAsQD_exciton_02nm.in -
-> 3DsphericGaAsQD_exciton_03nm.in -
-> 3DsphericGaAsQD_exciton_04nm.in -
-> 3DsphericGaAsQD_exciton_05nm.in -
-> 3DsphericGaAsQD_exciton_07nm.in -
-> 3DsphericGaAsQD_exciton_10nm.in -
3D nanocrystals (spherical quantum dots)
This tutorial aims to reproduce Figs. 1(a) and 1(b) of
Quantum confinement energies in zinc-blende III-V and group IV
semiconductors
G. Allan, Y.M. Niquet, C. Delerue
Applied Physics Letters 77 (5), 639 (2000)
We consider spherical GaAs nanocrystals that are surrounded by Ga2O3
barriers.
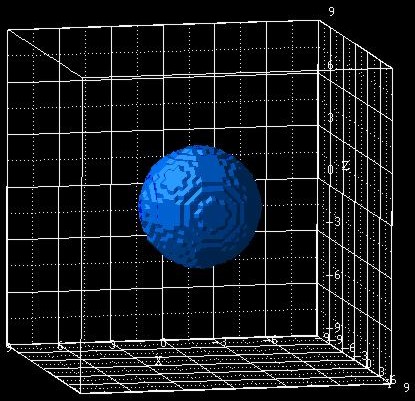
The following figure shows a GaAs nanocrystal with a diameter of 7 nm that is
surrounded by a cubic Ga2O3 matrix which has the size 18
nm x 18 nm.
The center of the spherical QD is located at (x,y,z) = (0,0,0).
To keep things simple, we assume isotropic and parabolic effective masses for
the electron and the heavy hole:
conduction-band-masses = 0.067d0 0.067d0 0.067d0 ! electron mass at Gamma conduction band
...
valence-band-masses = 0.5507d0
0.5507d0 0.5507d0 !
...
The heavy hole effective mass was obtained by spherically averaging over
all directions:
mhh,av = 1 / ( gamma1 - 0.8 gamma2 - 1.2
gamma3 ) = 0.5507
gamma1 = 6.98
gamma2 = 2.06
gamma3 = 2.93
The following figures show an isosurface (left figure) and contour plots of
2D slices (right figure) through the ground state electron wave function (psi≤)
of the 7 nm spherical GaAs nanocrystal.
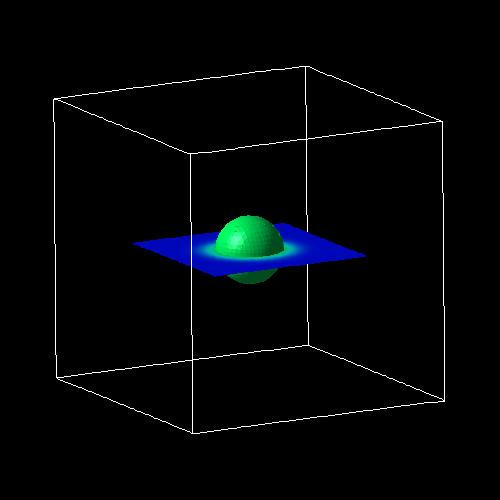 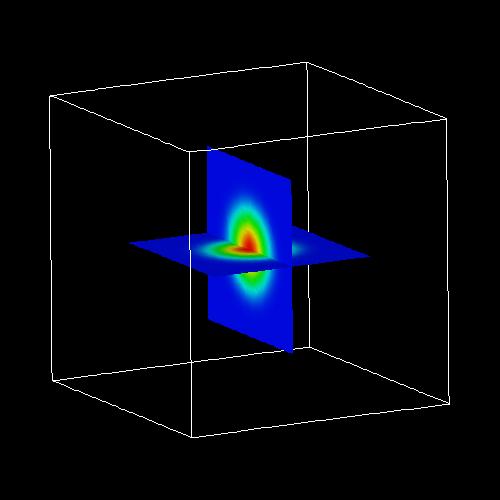
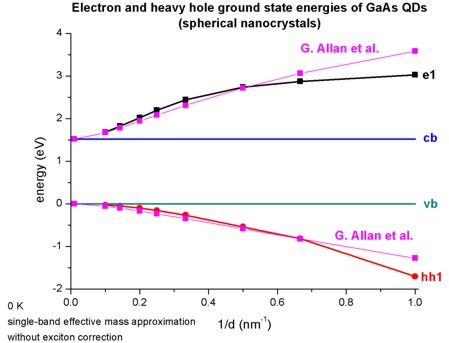
The following figure shows the energies of the electron ground state and the heavy hole
ground state in spherical GaAs nanocrystals as a function of the inverse of
the nanocrystal diameter d (d = 1 nm / 1.5 nm / 3 nm / 4 nm / 5 nm / 7 nm /
10 nm).
The energies of bulk GaAs are indicated by the constant lines (Ehh =
0 eV, Ecb = 1.519 eV).
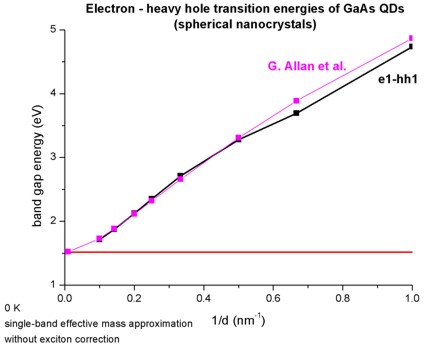
This figure shows the transition energies of the electron and the heavy hole
ground states in spherical GaAs nanocrystals as a function of the inverse of
the nanocrystal diameter d (d = 1 nm / 1.5 nm / 3 nm / 4 nm / 5 nm / 7 nm /
10 nm).
The energy of bulk GaAs is indicated by the constant line (Egap =
1.519 eV).
The transition energies can be found in this file:
Schroedinger_1band/interband3D_qc001_vb001_sg001_cb001_sg001_deg001_dir.dat
The following line is the relevant one where the second column shows the
transition energy in units of [eV]:
|<psi_vb001|psi_cb001_>|^2
2.123806789 0.800203758
Both figures are in very good agreement with Figs. 1(a) and 1(b) of
Quantum confinement energies in zinc-blende III-V and group IV
semiconductors
G. Allan, Y.M. Niquet, C. Delerue
Applied Physics Letters 77 (5), 639 (2000)
The only differences arise for very small nanocrystals having a diameter of
less than 1.5 nm.
Note that the calculated values do not include the exciton correction so far.
A more realistic calculation would take into account the anisotropy of the
heavy hole masses within a 6-band k.p model, or both, electron and heavy
hole anisotropies within an 8-band k.p model. Finally, the exciton
correction should be taken into account.
The energies for the above figures have been obtained using a 0.25 nm grid
resolution which is rather coarse. The use of a finer grid is thus recommended.
Exciton correction
The following flags are needed to include the exciton corrections:
$numeric-control
...
!---------
! Exciton
!---------
coulomb-matrix-element
= yes ! 'yes' or
'no'
calculate-exciton
= yes ! 'yes' or
'no'
exciton-iterations
= 10 ! e.g. 5
(for self-consistency loop)
exciton-residual
= 1d-6 ! e.g. 1d-5
exciton-electron-state-number
= 1 ! 1
=
exciton-hole-state-number
= 1 ! 1
=
!--------------------
! Exciton: X0
!--------------------
number-of-electron-states-for-exciton = 1
!
number-of-hole-states-for-exciton =
1 !
The energy of the exciton correction can be found in the file
Schroedinger_1band/exciton_energy3D.dat in the column Delta_Ex in units
of [eV].
|