|
| |
nextnano3 - Tutorial
next generation 3D nano device simulator
3D Tutorial
Exciton and biexciton corrections in idealistic 3D cubic quantum dots
Author:
Stefan Birner
If you want to obtain the input files that are used within this tutorial, please
check if you can find them in the installation directory.
If you cannot find them, please submit a
Support Ticket.
-> 3DcubicQD_exciton_04nm.in -
4 nm x 4 nm x 4 nm QD
-> 3DcubicQD_exciton_06nm.in -
-> 3DcubicQD_exciton_08nm.in -
-> 3DcubicQD_exciton_10nm.in -
-> 3DcubicQD_exciton_12nm.in -
-> 3DcubicQD_exciton_16nm.in -
-> 3DcubicQD_exciton_20nm.in -
-> 3DcubicQD_biexciton_04nm.in -
-> 3DcubicQD_biexciton_06nm.in -
-> 3DcubicQD_biexciton_08nm.in -
-> 3DcubicQD_biexciton_10nm.in -
-> 3DcubicQD_biexciton_12nm.in -
-> 3DcubicQD_biexciton_16nm.in -
-> 3DcubicQD_biexciton_20nm.in -
Exciton correction in idealistic 3D cubic quantum dots
- Here, we want to calculate the correction of the electron-hole transition
energies due to the exciton correction (Coulomb interaction of electron and
hole).
- The binding of the electron and the hole in a quantum dot is primarily due to
the conduction and valence band confinement. Thus the Coulomb interaction
between these two particles is just a small correction to the one-particle
energies. The magnitude of this energetic correction strongly depends on the
size of the quantum dot and the height of the confining barriers. Thus one would
expect a 1/r dependence (Coulomb potential) of the exciton correction in the
quantum dot.
- To test this, we calculate the exciton correction in an idealistic cubic 3D
InAs quantum dot. The band gap is assumed to be Egap = 0.417eV
(corresponding to a temperature of 0 K). The grid resolution was taken to be 0.5
nm, apart from the 20 nm dot where we took a grid resolution of 1 nm in order to
reduce CPU time.
We assumed infinite potential barriers at the quantum dot boundaries
which correspond to Dirichlet boundary conditions for the wave functions
at the quantum dot boundaries.
- To keep things simple, we assume isotropic and parabolic effective masses for
the electron and heavy hole:
conduction-band-masses =
0.026d0 0.026d0
0.026d0 ! electron mass at Gamma conduction band
...
valence-band-masses = 0.41d0
0.41d0 0.41d0 !
...
- The static dielectric constant is defined as follows:
static-dielectric-constants = 15.15d0
15.15d0 15.15d0 ! epsilon(0)
- Following the notation of the PhD thesis of O. Stier (TU Berlin) we have
to solve:
( H + Ve ) Psih = E'h Psih
( H + Vh ) Psie = E'e Psie
The exciton has the following ground state energy: EX = E'e
- E'h + C
C = ( < Psih | Ve | Psih
> - < Psie | Vh | Psie > ) / 2
The potentials Ve and Vh are obtained from the
relevant Poisson equations.
- exciton recombination energy: EX
(order of magnitude: ~ eV)
- exciton binding energy: The difference in energy
between the noninteracting single-particle states and the exciton energy: Ee
- Eh - EX
(order of magnitude: ~ meV)
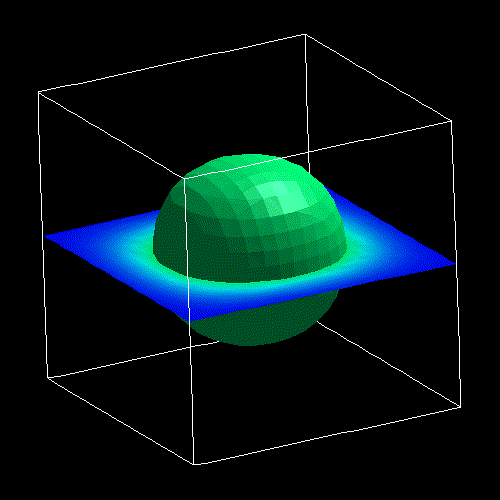
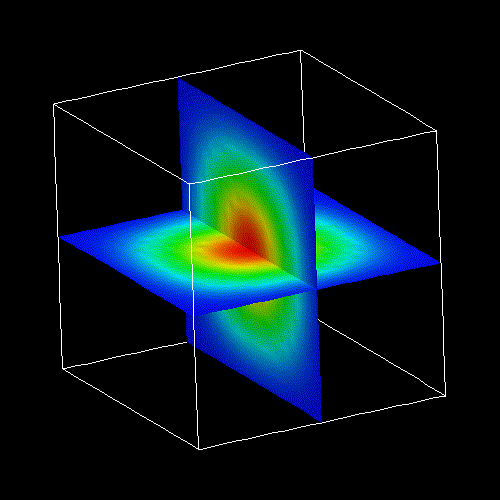
- The following figures show an isosurface and contour plots of 2D slices
through the ground state electron wave function (psi≤) of the 20 nm cubic InAs
quantum dot (without excitonic effects).
- The following flags are needed to include the exciton corrections:
$numeric-control
...
!---------
! Exciton
!---------
coulomb-matrix-element
= yes ! 'yes' or
'no'
calculate-exciton
= yes ! 'yes' or
'no'
exciton-iterations
= 10 ! e.g. 5
(for self-consistency loop)
exciton-residual
= 1d-6 ! e.g. 1d-5
exciton-electron-state-number
= 1 ! 1
=
exciton-hole-state-number
= 1 ! 1
=
!--------------------
! Exciton: X0
!--------------------
number-of-electron-states-for-exciton =
1
!
number-of-hole-states-for-exciton =
1 !
- The energy of the exciton correction can be found in the file
Schroedinger_1band/exciton_energy3Dcb001_vb001.dat in the column Delta_Ex
in units
of [eV].
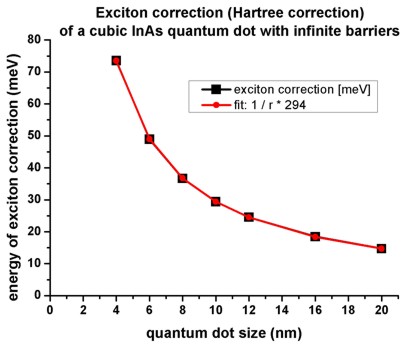
- The following figure shows the exciton correction due to the Coulomb
iteraction of the lowest electron state with the highest heavy hole state in
cubic InAs quantum dots as a function of quantum dot size (4 nm / 6 nm / 8 nm /
10 nm / 12 nm / 16 nm / 20 nm).
The curve clearly shows a 1/r dependence as expected from the Coulomb term
(indicated by the fitted curve).
- In addition to the correction in the electron and hole energies, the
wave functions will also change. This affects the transition matrix elements. Due
to the mutual attraction of electron and hole, the overlap of the wave functions
increases. This also reduces the influence of externally applied electric fields
(e.g. Quantum confined Stark shift).
Biexciton correction in idealistic 3D cubic quantum dots
- The biexciton consists of two electrons and two
holes.
exciton-electron-state-number
= 1 ! electron ground state
exciton-hole-state-number
= 1 !
!--------------------
! Biexciton: XX0
!--------------------
number-of-electron-states-for-exciton =
2 !
number-of-hole-states-for-exciton =
2 !
Following the notation of the PhD thesis of O. Stier (TU Berlin) we have to
solve:
( H + 2 Ve + Vh ) Psih =
E'h Psih
( H + Ve + 2 Vh ) Psie
= E'e Psie
The biexciton has the following ground state energy: EXX = 2 ( E'e
- E'h ) + 4C - Ce -
Ch
C = ( < Psih | Ve | Psih
> - < Psie | Vh | Psie > ) / 2
Ce = < Psie | Ve | Psie
>
Ch = - < Psih | Vh | Psih
>
The potentials Ve and Vh are obtained from the
relevant Poisson equations.
The following quantities are of interest:
- biexciton recombination energy: The transition from
biexciton ground state to exciton ground state: EXX -
EX
(order of magnitude: ~ eV)
- biexciton binding energy: The difference in
energy between two excitons and one biexciton: 2 EX -
EXX
(order of magnitude: ~ meV)
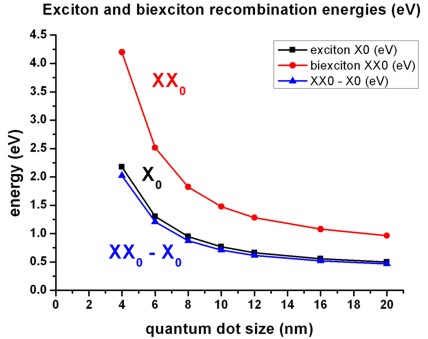
- The total energy of the exciton (X0) and the
biexciton (XX0) are shown in
the following figure (two-particle state). The energy of the biexciton is
roughly twice as large (four-particle state).
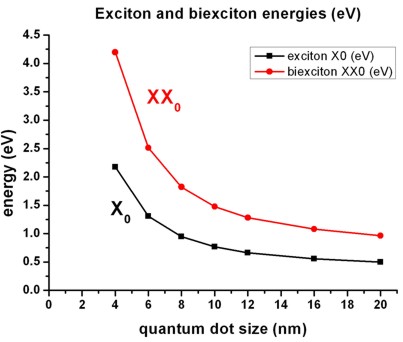
- X0 is the energy when the exciton recombines.
The biexciton recombination energy (XX0
- X0) is the energy when the biexciton is
subject to the transition from the biexciton ground state to the exciton
ground state.
This energy is similar to the energy X0.
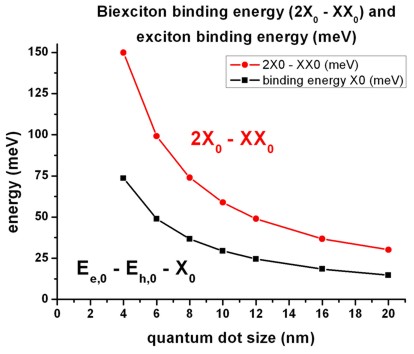
- The binding energy of the biexciton is shown in comparison to the
exciton binding energy.
Ee,0 and Eh,0 are the electron and hole one-particle
energies (without excitonic corrections).
- More details on the biexciton:
$numeric-control
|