www.nextnano.com/documentation/nextnanoplus_tutorials/
nextnano3 - Tutorial
next generation 3D nano device simulator
1D Tutorial
Intersubband transitions in InGaAs/AlInAs multiple quantum well systems
Authors:
Stefan Birner
-> 1DSirtoriPRB1994_OneWell_sg_self-consistent_nn3.in
/ *_nnp.in - (single-band effective mass approximation)
-> 1DSirtoriPRB1994_OneWell_sg_quantum-only_nn3.in
/ *_nnp.in -
-> 1DSirtoriPRB1994_OneWell_kp_quantum-only_nn3.in
/ *_nnp.in -
-> 1DSirtoriPRB1994_TwoCoupledWells_sg_self-consistent_nn3.in /
*_nnp.in -
-> 1DSirtoriPRB1994_TwoCoupledWells_sg_quantum-only_nn3.in
/ *_nnp.in -
-> 1DSirtoriPRB1994_TwoCoupledWells_kp_quantum-only_nn3.in
/ *_nnp.in -
-> 1DSirtoriPRB1994_ThreeCoupledWells_sg_self-consistent_nn3.in / *_nnp.in
-
-> 1DSirtoriPRB1994_ThreeCoupledWells_sg_quantum-only_nn3.in /
*_nnp.in -
-> 1DSirtoriPRB1994_ThreeCoupledWells_kp_quantum-only_nn3.in
/ *_nnp.in -
These input files are included in the latest version.
Intersubband transitions in InGaAs/AlInAs multiple quantum well systems
This tutorial aims to reproduce Figs. 4 and 5 of
C. Sirtori, F. Capasso, J. Faist
Nonparabolicity and a sum rule associated with bound-to-bound
and bound-to-continuum intersubband transitions in quantum wells
Physical Review B 50 (12), 8663
(1994)
This tutorial nicely demonstrates that for the ground state energy the
single-band effective mass approximation is sufficient whereas for the higher
lying states a nonparabolic model, like the 8-band k.p approximation, is
necessary.
This is important for e.g. quantum cascade lasers where higher lying
states have a dominant role.
Step1: Layer sequence
We investigate three structures:
a) a single quantum well
b) two coupled quantum wells
c) three coupled quantum wells
Step 2: Material parameters
We use In0.53Ga0.47As as the quantum well material and
Al0.48In0.52As as the barrier material. Both materials are
lattice matched to the substrate material InP. Thus we assume that the InGaAs
and AlInAs layers are unstrained with respect to the InP substrate.
The paper
C. Sirtori, F. Capasso, J. Faist
Nonparabolicity and a sum rule associated with bound-to-bound
and bound-to-continuum intersubband transitions in quantum wells
Physical Review B 50 (12), 8663
(1994)
lists the following material parameters:
| conduction band offset |
Al0.48In0.52As/In0.53Ga0.47As |
0.510 eV |
| conduction band effective mass |
(In0.53Ga0.47As) |
0.043 m0 |
| conduction band effective mass |
(Al0.48In0.52As) |
0.072 m0 |
The temperature is set to 10 Kelvin.
Step 3: Method
Single-band effective mass approximation
Because our structure is doped, we have to solve the single-band
Schrödinger-Poisson equation self-consistently.
The doping is such that the electron ground state is below the Fermi level and
all other states are far away from the Fermi level, i.e. only the ground state
is occupied and contributes to the charge density.
$simulation-flow-control
flow-scheme = 2
raw-potential-in = no
$quantum-model-electrons
...
model-name
= effective-mass
number-of-eigenvalues-per-band = 3
! Note: Single-band eigenstates are two-fold spin
degenerate.
The Fermi level is always equal to 0 eV in our simulations and the band profile
is shifted accordingly to meet this requirement.
8-band k.p approximation
Old version of this tutorial:
Becauce both, the single-band and the 8-band k.p ground state energy
and the corresponding wave functions are almost identical, we can read in the
self-consistently calculated electrostatic potential of the single-band
approximation and calculate for this potential the 8-band k.p eigenstates
and wave functions for k|| = 0.
$simulation-flow-control
flow-scheme =
3
raw-directory-in =
raw_data/
raw-potential-in =
yes
$quantum-model-electrons
...
model-name
= 8x8kp
number-of-eigenvalues-per-band = 6
! Note: One k.p eigenstate for each spin component.
New version of this tutorial:
We provide input files for:
a) self-consistent single-band Schrödinger equation (because the structure
is doped)
b) single-band Schrödinger equation (without self-consistency)
c) 8-band k.p single-band Schrödinger equation (without
self-consistency)
For a), although the structure is doped, the band bending is very small.
Thus we omit for the single-band / k.p comparison in b) and c)
the self-consistent cycle.
Step 4: Results
- Single quantum well
The following figure shows the lowest two electron eigenstates for an In0.53Ga0.47As/Al0.48In0.52As
quantum well structure calculated with single-band effective mass
approximation and with a nonparabolic 8-band k.p model. The energies (and
wave functions, i.e. psi²) for the ground state are identical in both models
but the second eigenstate differs substantially. Clearly the single-band model
leads to an energy which is far too high for the upper state. Our calculated
value for the intersubband transition energy E12 of 255 meV
compares well with both, the calculated value of Sirtori et al. (258 meV) and
their measured value (compare with absorption curve in Fig. 4 of their paper).
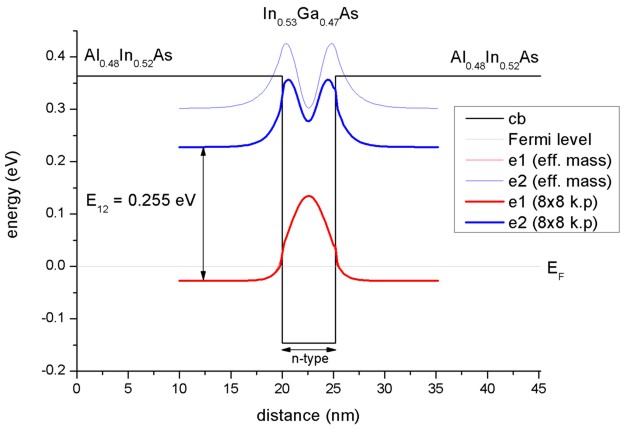
The calculated intersubband dipole moments are:
z12 = 1.55 nm (single-band)
z12 = ... nm (8-band k.p)
(Sirtori's paper: 1.53 nm (exp.), 1.48 nm (th.)).
The influence of doping on the eigenenergies is negligible (smaller than 1
meV).
- Two coupled quantum wells
The following figure shows the lowest three electron eigenstates for an In0.53Ga0.47As/Al0.48In0.52As
double quantum well structure calculated with single-band effective mass
approximation and with a nonparabolic 8-band k.p model. The energies (and
wave functions, i.e. psi²) for the ground state are very similar in both models
but the second and especially the third eigenstate differ substantially.
Clearly the single-band model leads to energies which are far too high for the
higher lying states. Our calculated values for the intersubband transition
energies E12 = 150 meV and E13 = 267 meV compare well
with both, the calculated values of Sirtori et al. (150 meV and 271 meV) and
their measured values (compare with absorption curve in Fig. 5 (a) of their
paper).
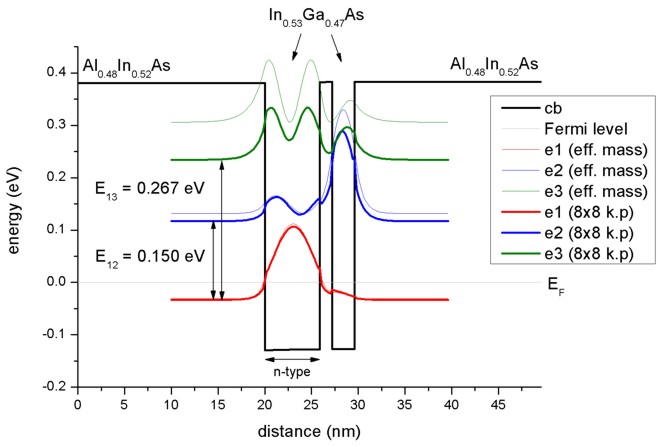
The calculated intersubband dipole moments are:
z12 = 1.61 nm (single-band)
z13 = 1.11 nm (single-band)
z12 = ... nm (8-band k.p)
z13 = ... nm (8-band k.p)
(Sirtori's paper: z12 = 1.64 nm (exp.), z12 = 1.65
nm (th.))
The influence of doping on the eigenenergies is almost negligible (between 0
and 2 meV).
- Three coupled quantum wells
The following figure shows the lowest four electron eigenstates for an In0.53Ga0.47As/Al0.48In0.52As
triple quantum well structure calculated with single-band effective mass
approximation and with a nonparabolic 8-band k.p model. The energies (and
wave functions, i.e. psi²) for the ground state are similar in both models but
the second and especially the third and forth eigenstates differ
substantially. Clearly the single-band model leads to energies which are far
too high for the higher lying states. Our calculated values for the
intersubband transition energies E12 = 118 meV, E13 =
261 and E14 = 370 meV compare well with both, the calculated values
of Sirtori et al. (116 meV, 257 meV and 368 meV) and their measured values
(compare with absorption curve in Fig. 5 (b) of their paper).
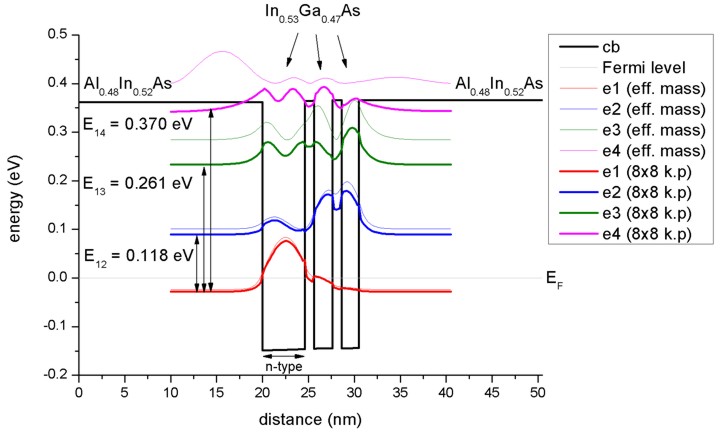
The calculated intersubband dipole moments are:
z12 = 1.81 nm (single-band)
z13 = 0.77 nm(single-band)
z14 = 0.30 nm(single-band)
z12 = ... nm (8-band k.p)
z13 = ... nm (8-band k.p)
z14 = ... nm (8-band k.p)
(Sirtori's paper: z12 = 1.86 nm (exp.), z12 = 1.84
nm
(th.))
The influence of doping on the eigenenergies is almost negligible (between 0
and 4 meV).


