1D Double Quantum Well

nextnano.com
nextnano³
Download | Search | Copyright | Publications
* password protected

nextnano³ software

Double Quantum Well

This tutorial aims to reproduce two figures (Figs. 3.16, 3.17, p. 92) of Paul Harrison's excellent book "Quantum Wells, Wires and Dots" (Section 3.9 "The Double Quantum Well"), thus the following description is based on the explanations made therein.
We are grateful that the book comes along with a CD so that we were able to look up the relevant material parameters and to check the results for consistency.

Double Quantum Well: AlGaAs / 6 nm GaAs / 4 nm AlGaAs / 6 nm GaAs / AlGaAs

Our symmetric double quantum well consists of two 6 nm GaAs quantum wells, separated by a 4 nm Al_0.2Ga_0.8As barrier and surrounded by 20 nm Al_0.2Ga_0.8As barriers on each side.
We thus have the following layer sequence: 20 nm Al_0.2Ga_0.8As / 6 nm GaAs / 4 nm Al_0.2Ga_0.8As / 6 nm GaAs / 20 nm Al_0.2Ga_0.8As.
The barriers are printed in bold.

This figure shows the conduction band edge and the lowest two electron eigenenergies and wave functions that are confined inside the wells.
(Note that the energies were shifted so that the conduction band edge of GaAs equals 0 eV.)

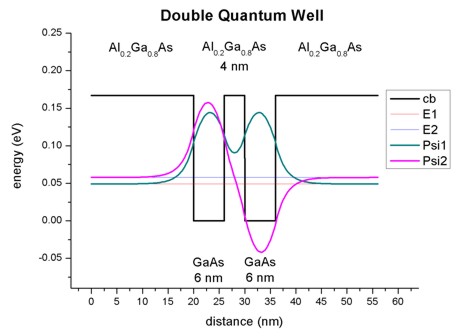
The wave functions form a symmetric and an anti-symmetric pair. The symmetric one is lower in energy than the anti-symmetric one.
The plot is in excellent agreement with Fig. 3.17 (page 92) of Paul Harrison's book "Quantum Wells, Wires and Dots".

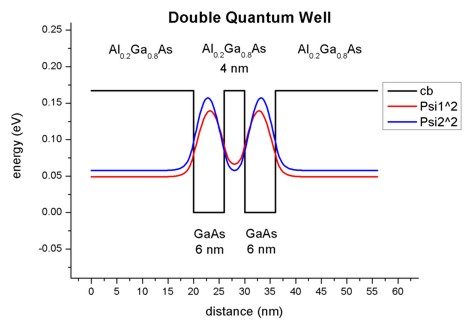
For comparison, the following figure shows for the same structure as above, the square of the wave function rather than Psi only.

Output

a) The conduction band edge of the Gamma conduction band can be found here:

  band_structure / cb_Gamma.dat

b) This file contains the eigenenergies of the two lowest eigenstates. The units are [eV].



  Schroedinger_1band / ev_cb1_qc1_sg1_deg1.dat

nextnano³:

       
  num_ev:  eigenvalue [eV]:

                      
  1        0.04920

                      
  2        0.05779

nextnano++:

       
  num_ev:  eigenvalue [eV]:

                      
  1        0.04920

                      
  2        0.05779

Paul Harrison's book:

1        
  0.04912

                      
  2        0.05770

c) This file contains the eigenenergies and the squared wave functions (Psi²):



  Schroedinger_1band / cb1_qc1_sg1_deg1_psi_squared_shift.dat

This file contains the eigenenergies and the wave functions (Psi):



  Schroedinger_1band / cb1_qc1_sg1_deg1_psi_shift.dat

The subscript

 _shift

indicates that Psi² and Psi are shifted by the corresponding energy levels.

a) and c) can be used to plot the data as shown in the figures above.

Double Quantum Well: AlGaAs / 6 nm GaAs / ... nm AlGaAs / 6 nm GaAs / AlGaAs

Here, we varied the thickness (from 1 nm to 14 nm) of the Al_0.2Ga_0.8As barrier layer that separates the two quantum wells and calculated the energies of the two lowest eigenstates. The width of the quantum wells is fixed (6 nm).

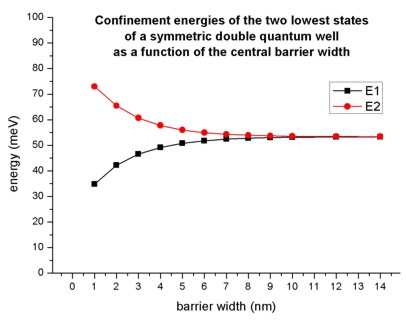
If the separation between the two quantum wells is large, the wells behave as two independent single quantum wells having the identical ground state energies. The interaction between the energy levels localized within each well increases once the distance between the two wells decreases below 10 nm. One state is forced to higher energies and the other to lower energies. Here, the electron spins align in an "anti-parallel" arrangement in order to satisfy the Pauli exclusion principle.

This is analogous to the hydrogen molecule where the formation of a pair of bonding and anti-bonding orbitals occurs once the two hydrogen atoms A and B are brought together.
Psi_bonding = 1/SQRT(2) ( Psi_A + Psi_B ) (lower energy)
Psi_anti-bonding = 1/SQRT(2) ( Psi_A - Psi_B ) (higher energy)

Again, the plot is in excellent agreement with Fig. 3.16 (page 92) of Paul Harrison's book "Quantum Wells, Wires and Dots".

Output: The energy values were taken from this file:



  Schroedinger_1band / ev_cb1_qc1_sg1_deg1.dat

For example, the values for the 1 nm barrier read:

nextnano³:

       
  num_ev:  eigenvalue [eV]:

                      
  1        0.03476

                      
  2        0.07298

nextnano++:

       
  num_ev:  eigenvalue [eV]:

                      
	1        0.03476

                      
	2        0.07298

Paul Harrison's book:

1        
  0.03470

                      
  2        0.07290

The values for the 14 nm barrier read:

nextnano³:

       
  num_ev:  eigenvalue [eV]:

                      
	1        0.05332

                      
  2        0.05338

nextnano++:

       
  num_ev:  eigenvalue [eV]:

                      
	1        0.05332

                      
	2        0.05338

Paul Harrison's book:

1        
  0.05323

                      
  2        0.05329

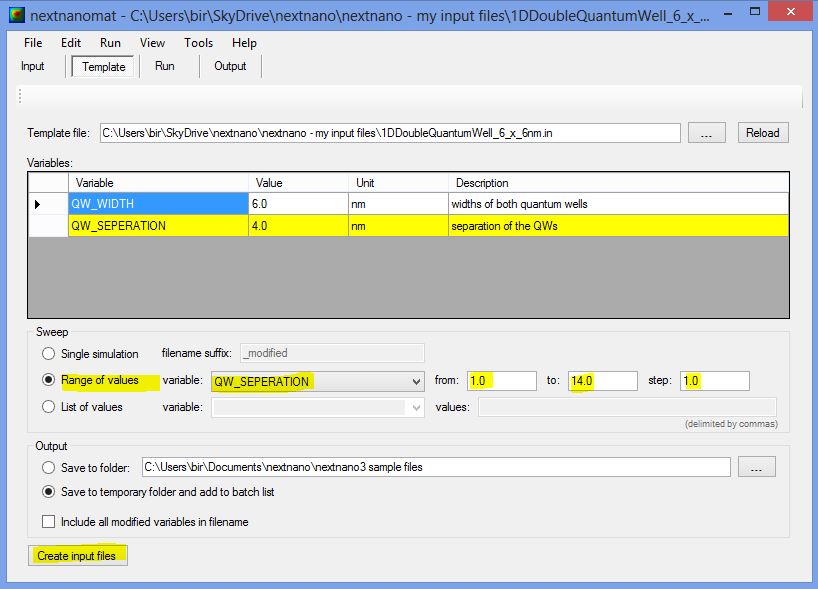
A sweep over the thickness of the Al_0.2Ga_0.8As barrier layer, i.e. the variable %QW_SEPARATION, can be done easily by using nextnanomat's Template feature.
The following screenshot shows how this can be done.
Go to "Template", open input file, select "Range of values", select "QW_SEPARATION", click on "Create input files", go to "Run and start your simulations.

Another tutorial on coupled quantum wells can be found here.

nextnano³ - Tutorial

1D Tutorial

Double Quantum Well

Double Quantum Well

Double Quantum Well: AlGaAs / 6 nm GaAs / 4 nm AlGaAs / 6 nm GaAs / AlGaAs

Double Quantum Well: AlGaAs / 6 nm GaAs / ... nm AlGaAs / 6 nm GaAs / AlGaAs

nextnano3 - Tutorial

1D Tutorial

Double Quantum Well

Double Quantum Well

Double Quantum Well: AlGaAs / 6 nm GaAs / 4 nm AlGaAs / 6 nm GaAs / AlGaAs

Double Quantum Well: AlGaAs / 6 nm GaAs / ... nm AlGaAs / 6 nm GaAs / AlGaAs

nextnano³ - Tutorial