nextnano³ - Tutorial

next generation 3D nano device simulator

1D Tutorial

Electron density of states (DOS) of a GaAs quantum well with infinite barriers and
hole density of states (DOS) of a Si hole channel (triangular potential)

Author: Stefan Birner

If you want to obtain the input files that are used within this tutorial, please check if you can find them in the installation directory.
If you cannot find them, please submit a Support Ticket.
-> 1D_DOS_GaAsQW_10nm.in -> 1D_DOS_GaAsQW_20nm.in -> 1D_DOS_GaAsQW_100nm.in -> 1DSi_triangular_DOS_holes.in

1) Electron density of states (DOS) of a GaAs quantum well with infinite barriers

-> 1D_DOS_GaAsQW_10nm.in -> 1D_DOS_GaAsQW_20nm.in -> 1D_DOS_GaAsQW_100nm.in

Here, we calculate the density of states (DOS) for the electrons in a 10 nm, 20 nm and 100 nm GaAs quantum well using infinite barriers.

We are using the 8-band k.p model and calculate the energy dispersion E(k_||) = E(k_x,k_y).
However, for simplicity, and in order to be able to check our k.p results with analytical results of the single-band approximation (i.e. parabolic and isotropic energy dispersion), we modify our 8-band k.p parameters so that the coupling between electrons and holes is switched off. Consequently, we are using an isotropic and parabolic effective mass of 0.067 [m₀] for our 8-band k.p model.

The density of states for a single subband in a (GaAs) quantum well system can be calculated to be:
rho^2D(E) = m*            / (pi h_bar²) =
             = 0.067 [m₀] / (pi h_bar²) =
             = 0.067 * 2.607275116 * 10³⁷ J^-1 m^-2 =
             = 0.067 * 4.177314998 * 10¹⁸ eV^-1 m^-2 =
             = 1.746874328 * 10³⁶ J^-1 m^-2 =             = 2.798801048 * 10¹⁷ eV^-1 m^-2

[m₀] / (pi h_bar²) = 2.607275116 * 10³⁷ J^-1 m^-2 = 4.177314998 * 10¹⁸ eV^-1 m^-2

The following figure shows the electron density of states (DOS) as a function of energy for a GaAs QW with infinite barriers.
The QW width has been assumed to be L_z = 10 nm, L_z = 20 nm and L_z = 100 nm.
In order to compare the four cases
- 10 nm QW
- 20 nm QW
- 100 nm QW
- bulk (analytical formula)
we scale rho^2D(E) by dividing by the length of the QW: rho^{2D '}(E) = rho^2D(E) / L_z
where L_z is the length of the QW. Then rho^{2D '} in units of eV^-1 m^-3.

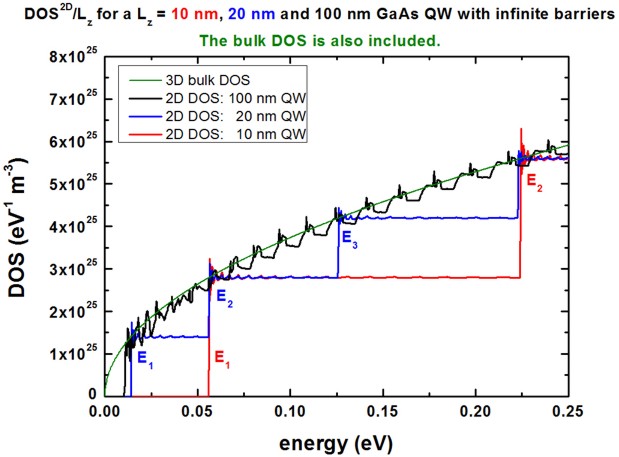
For a QW, a sharp steplike density of states is obtained, in contrast to the bulk case where a E^1/2 dependence is expected.
(The bulk curve has been calculated analytically.)
Our results are in excellent agreement with analytical results for the two-dimensional DOS (e.g. compare with P. Harrison, Quantum wells, wires and dots or S.L. Chuang, Physics of optoelectronic devices).

The DOS output is contained in the following file: DOS_el_sum_norm.dat
The first column contains the energy in units of [eV], the second column the DOS (sum over all subbands) in units of [eV^-1 m^-2].
The DOS output for each individual subband is contained in this file:DOS_el_norm.datThe first column contains the energy in units of [eV], the other columns the DOS of each individual subband in units of [eV^-1 m^-2].

Note: The nextnano³ output DOS_el_sum.dat depends on the size of the k_|| space region: ~ 1 / k_||,max² For this output, it seems that the spin is included twice. So these values have to be divided by "2".
The nextnano³ outputDOS_el_sum_norm.dat does not depend on the size of the k_|| space region. The spin factor is correct.

The following parameters were used:

10 nm QW: 0.25 nm grid resolution; 3000 k_|| points in total, i.e. 351 k_|| have to be calculated
20 nm QW: 0.50 nm grid resolution; 3000 k_|| points in total, i.e. 351 k_|| have to be calculated
100 nm QW: 1.00 nm grid resolution; 3000 k_|| points in total, i.e. 351 k_|| have to be calculated

The following interesting question arises:

How does the DOS look like for a QW with finite barriers and an anisotropic and nonparabolic effective mass tensor (8-band k.p)?

Comment: There are different definitions of the density of states.

P. Harrison: rho^2D(E) = m* / (pi h_bar²)
G. Bastard: rho^2D(E) = m* / (pi h_bar²) * L_x L_y
S.L. Chuang: rho^2D(E) = m* / (pi h_bar²) / L_z

Other results (benchmark):

Paul Harrison for a 20 nm GaAs QW with infinite barriers:
1.746847 * 10³⁶ J^-1 m^-2 = 2.798757 * 10¹⁷ eV^-1 m^-2 for an electron mass of m* = 0.067 [m₀].
This corresponds to rho^{2D '}(E) = rho^2D(E) / L_z = 1.399 * 10²⁵ eV^-1 m^-3 f
S.L. Chuang for a 10 nm GaAs QW (p. 90) at the first step (E₁ = 56.5 meV): 2.78 * 10²⁵ eV^-1 m^-3
S.L. Chuang for bulk GaAs (p. 90): 100 meV above E_c: 3.69 * 10²⁵ eV^-1 m^-3

2) Hole density of states (DOS) of a Si hole channel (triangular potential)

-> 1DSi_triangular_DOS_holes.in

Here, we calculate the density of states (DOS) for the holes in a 10 nm wide Si channel that is modeled by a triangular potential, corresponding to an applied electric field of 5 MV/cm.

A 1 nm SiO₂ oxide layer is included in the simulations.
The Si/SiO₂ valence band offset (VBO) was assumed to be 4.3 eV.
The grid spacing in real space was 0.1 nm.
The following 6-band k.p parameters are employed for both the Si and the SiO₂ layer:
6x6kp-parameters = -6.53d0 -4.64d0 -8.32d0 ! L, M, N 0.044d0 !Delta_split-off[eV]Note that our L, M, N parameters are the same as in
M.V. Fischetti, JAP 80, 2234 (1996)
but Fischetti's parameters (L',M',N) have to be converted because his parameters are defined differently. ==> L = L' - 1, M = M' - 1, N = N'
The energy dispersion E(k_x,k_y) is discretized on a square up to k_x,max = k_y,max = 0.7 [1/Angstrom]
k-range = 0.7d0 ! [1/Angstrom]
num-kp-parallel = 4761 ! 4761 = 595 x 8 + 1using a total of 4761 points in the two-dimensional (k_x,k_y) space.
Due to symmetry, we only have to discretize ~1/8^th of the total 2D k_|| space, i.e. the 6-band k.p Hamiltonian (dimension of matrix: 600 x 600) has to be diagonalized 595 times.

This tutorial is similar to the following paper:

Hole transport in p-channel Si MOSFETs
S. Krishnan, D. Vasileska, M.V. Fischetti
Microelectronics Journal 36, 323 (2005)

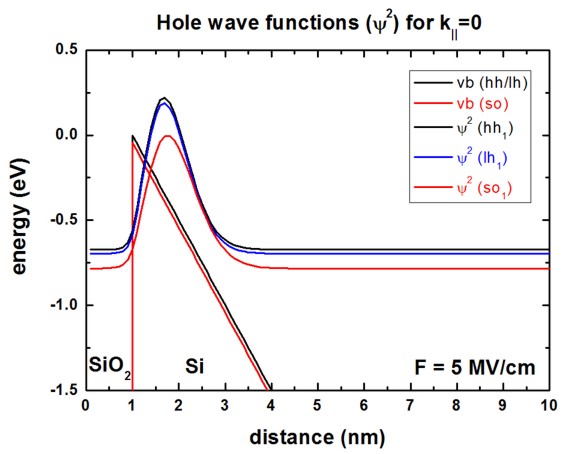
The following figure shows the valence band edges of heavy, light and split-off hole at an electric field of 5 MV/cm.
The heavy and light hole valence band edges are degenerate because the silicon layer is assumed to be unstrained.
The square of the wave functions of the heavy hole, light hole and split-off hole are also shown.
At k_|| = 0, the energies and the squares of the spin-up and spin-down wave functions are identical.
This is not the case for k_|| /= 0 because the quantum well potential is unsymmetric.

The following figure shows the two-dimensional density of states (DOS) for the holes in the 10 nm triangular Si channel at an electric field of 5 MV/cm.
At k_|| /= 0 the energies for spin-up and spin-down states are not equal any more leading to different DOS for spin-up and spin-down.
Here, we want to emphasize the different DOS for heavy hole, light hole and split-off hole (thus we added the spin-up and spin-down DOS for each subband).
One can nicely see that the hole DOS differs dramatically from the step-like DOS of the analytical isotropic and parabolic effective-mass approximation. Only the heavy hole DOS is close to this simple approximation.

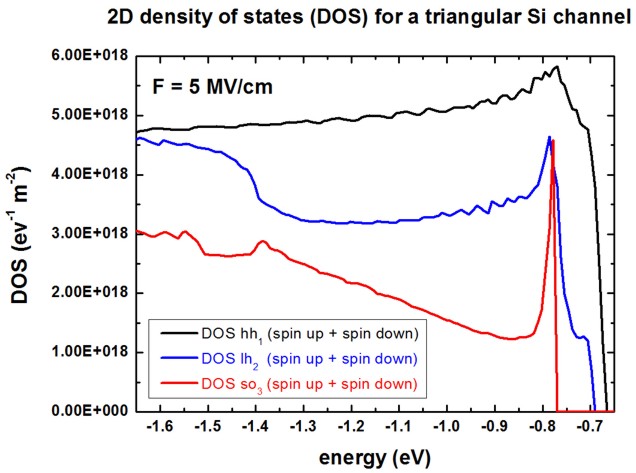
With respect to this energy scale, the valence band maximum is located at 0 eV.
At k_|| = 0,
- the top-most heavy hole state is atE_hh1 = -0.672 eV
- the top-most light hole state is atE_lh1 = -0.696 eV -the top-most split-off hole state is at E_so1 = -0.784 eV.Obviously, between 0 eV and the top-most state, the DOS is zero for this subband.

Our heavy and light hole DOS is in good agreement with the paper of Krishnan et al. However, the split-off hole DOS differs.
Namely, it is not clear why Krishnan's split-off hole DOS seems to start at an energy which is equal to the heavy hole energy.

See also this tutorial for more information on the energy dispersion E(k_x,k_y) of a triangular Si channel:
k_|| energy dispersion of holes in unstrained and strained silicon inversion layers