|
| |
nextnano3 - Tutorial
next generation 3D nano device simulator
1D Tutorial
Strain: Band shifts and splittings due to conduction and valence band
deformation potentials
Author:
Stefan Birner
If you want to obtain the input files that are used within this tutorial, please
check if you can find them in the installation directory.
If you cannot find them, please submit a
Support Ticket.
-> 1Ddeformation_potentials_no_strain_nn3.in / *_nnp.in -
input file for the nextnano3 and nextnano++ software
-> 1Ddeformation_potentials_strain_nn3.in / *_nnp.in -
-> 1Ddeformation_potentials_ReadInStrainTensor_hydro_nn3.in / *_nnp.in -
-> 1Ddeformation_potentials_hydro.in -
InAs/GaAs/InAs structure
- This input file simulates an InAs/GaAs/InAs structure.
The structure is grown pseudomorphically on InAs, i.e. the GaAs is
tensilely strained, the InAs is unstrained. The growth direction [001]
is along z, the interfaces are in the (x,y) plane.
- We artificially set the electrostatic potential to zero to avoid any
further shifting of
the band edges.
By default Varshni parameters are used to determine temperature dependent
band gaps
(i.e. temperature dependent conduction-band-energies).
Here, the Varshni parameters are switched off, thus the conduction and valence
band edges from the database (or input file) are taken.
$numeric-control
simulation-dimension
= 1
zero-potential
= yes
varshni-parameters-on = no !
lattice-constants-temp-coeff-on = no !
Lattice constants independent of temperature.
Absolute values from database are taken.
$end_numeric-control
No strain
-> 1Ddeformation_potentials_no_strain.in
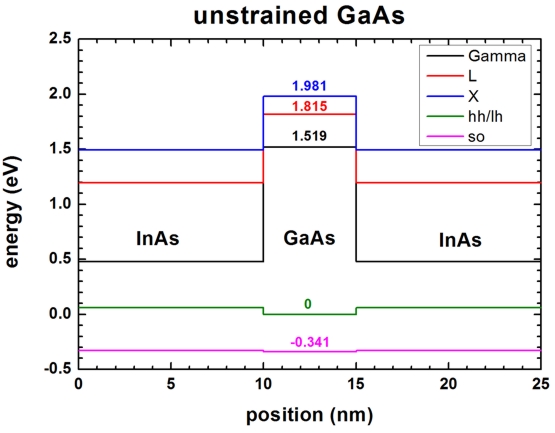
- The following figure shows the conduction and valence band edges of the
heterostructure when no strain is applied (
strain-calculation =
no-strain). The heavy and
light hole bands are degenerate.
- GaAs:
conduction-band-energies = 2.979d0 3.275d0
3.441d0 ! [eV] Gamma, L, X
valence-band-energies =
1.346d0
! [eV] Ev,av
6x6kp-parameters =
... ...
... !
0.341d0 ! [eV] Deltasplit-off
Conduction bands:
-> Gamma
band = 2.979
-> L
band = 3.275
-> X
band = 3.441
Valence bands:
-> heavy hole band =
1.346 + 1/3 * 0.341 = 1.45967
(= Ev,av + 1/3 *
Deltasplit-off =
Ev,max)
-> light hole band =
1.346 + 1/3 * 0.341 = 1.45967
(= Ev,av + 1/3 *
Deltasplit-off =
Ev,max)
-> split-off hole band = 1.346 -
2/3 * 0.341 = 1.11867 (= Ev,av
- 2/3 *
Deltasplit-off =
Ev,max -
Deltasplit-off)
Note: We apply an overall band-shift to all bands in order to align the
topmost valence bands (heavy hole/light hole) to zero (0 eV).
!-----------------------------------------------
! Shift all bands, so that GaAs (hh/lh) = 0 eV. ==>
Ev,max = 0
!-----------------------------------------------
band-shift = -1.45967d0 ! [eV]
-> Gamma
band = 2.979 - 1.45967 =
1.519
-> L
band = 3.275 - 1.45967 =
1.815
-> X
band = 3.441 - 1.45967 = 1.981
Valence bands:
-> heavy hole band =
1.45967 - 1.45967 =
0 (=
Ev,max)
-> light hole band =
1.45967 - 1.45967 =
0 (=
Ev,max)
-> split-off hole band = 1.11867 -
1.45967 = -0.341
For details of the calculations of the band gap or band edges see
FAQ section.
Strain (biaxial strain)
-> 1Ddeformation_potentials_strain.in
- Then we turn on strain (
strain-calculation =
homogeneous-strain). Here it is
interesting to see that the six-fold degenerate X bands in GaAs split.
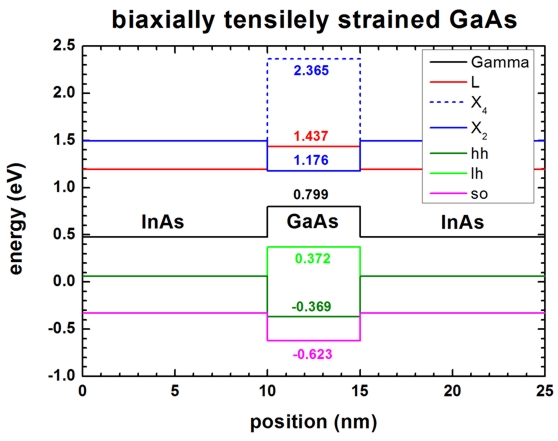
- Valence bands
absolute-deformation-potential-vb =
-1.21d0 ! av [eV]
uniax-vb-deformation-potentials =
-2.0d0 ...
! b,d [eV]
InAs has a larger lattice constant than GaAs.
The tensile strain for GaAs has the following three components (the
offdiagonal strain components are zero):
e|| = exx = eyy = 0.07165
e_|_ = ezz = - 0.06643
The hydrostatic strain is the trace of the strain tensor and
corresponds to the change in volume dV/V:
ehydro = Tr(eij) = exx + eyy + ezz
= 2e|| + e_|_ = 0.07687
The three valence bands shift by a constant amount (hydrostatic or absolute
deformation potential):
Ev,av' = Ev,av + av ehydro
= Ev,av + (-1.21 ehydro) =
Ev,av - 0.0930127
In addition to this shift each hole band gets a further shift which depends on
the growth direction: For growth direction along [001] the additional valence
bands shift in the following way:
Ev*(hh) = - 1/2 Esh001
Ev*(lh) = - 1/2 Deltaso + 1/4 Esh001
+ 1/2 [ SQRT(Deltaso2 + Deltaso Esh001
+ 9/4 (Esh001)2 ) ]
Ev*(so) = - 1/2 Deltaso + 1/4 Esh001
- 1/2 [ SQRT(Deltaso2 + Deltaso Esh001
+ 9/4 (Esh001)2 ) ]
These three equations include the spin-orbit split-off energy
Deltaso
and are thus given relative to the unstrained valence band edge
maximum
Ev,max =
Ev(hh) = Ev(lh).
Ev*(hh) = 0
Ev*(lh) = 0
Ev*(so) = - Deltaso
Esh001 = -b(exx + eyy - 2ezz)
= 2b(e_|_-e||) = 2(-2.0)(e_|_-e||)
= 0.55232
Ev(hh) =
Ev,max + av ehydro
+ Ev*(hh) =
Ev,max
- 0.0930127 + ( -
0.27616 )
= -0.369
Ev(lh) =
Ev,max + av ehydro
+ Ev*(lh) =
Ev,max
- 0.0930127 + ( -
0.1705 + 0.13808 + 0.497745 ) = 0.372
Ev(so) =
Ev,max + av ehydro
+ Ev*(so) =
Ev,max - 0.0930127
+ ( - 0.1705 +
0.13808 - 0.497745 ) = -0.623
In our example, we have shifted the bands (band-shift = -1.45967d0),
so that it holds for unstrained GaAs:
Ev,max
= 0
- Conduction bands
absolute-deformation-potentials-cbs = -9.36d0 -4.91d0 -0.16d0
! ac(Gamma), ac(L),
ac(X)
uniax-cb-deformation-potentials =
0d0 14.26d0 8.61d0 !
Xi(Gamma), Xi(L), Xi(X)
Ec'(Gamma) = Ec0(Gamma) + ac(Gamma)
ehydro = Ec0(G) + (-9.36
ehydro) = 1.519 - 0.7195 =
0.799
Ec'(L) = Ec0(L)
+ ac(L) ehydro = Ec0(L)
+ (-4.91 ehydro) =
1.815
- 0.3774 = 1.437
Ec'(X) = Ec0(X)
+ ac(X) ehydro = Ec0(X)
+ (-0.16 ehydro) =
1.981
- 0.0123 = 1.9687
The X conduction band of GaAs is also subjected to a splitting (upwards and
downwards relative to Ec'(X)). This amount depends on
the growth direction. For [001] growth direction the splitting is given by
Ec001*(X) = 2/3
Xi(X) (e_|_-e||) = 2/3 *
8.61 * (-0.13808) = - 0.7925792
Ec100,010*(X) = - 1/3 Xi(X) (e_|_-e||)
= - 1/3 * 8.61 * (-0.13808) = 0.3962896
--> Ec001(X) = Ec'(X)
+ Ec001* (X) = 1.9687 - 0.7925792 =
1.176 (2-fold valley degeneracy)
--> Ec100,010(X) = Ec'(X) + Ec100,010*(X)
= 1.9687 + 0.3962896 = 2.365
- The above given equations for the valence band are not used
inside nextnano≥, however. We get the band shifts by diagonalizing the
Bir-Pikus strain Hamiltonian which is given in
Basics 2 (strain
effects). This is a more general approach as it gives the correct shifts
for arbitrary orientations (However, it is only for valence bands). The
equations above are the special case for growth along the [001] direction.
- Note: There are two different definitions of the valence band
deformation potential in the literature. What can be measured experimentally
is the deformation potential of the band gap which is composed of the
deformation potential of the valence and conduction band edge.
agap = ac + av
(e.g. definition in
Vurgaftman1)
One can also argue that the conduction band deformation potential can be
constructed from the valence band edge and the band gap deformation potential
like this:
ac = av + agap
(definition in nextnano≥)
The equations differ in the sign of the valence band deformation potential.
Note that the Erratum of
Bahder1 is not in agreement with the definiton inside nextnano≥.
Note also the comment of
Vurgaftman1: "... the band gap increases for a compressive strain. Under
positive hydrostatic pressure, i.e. negative strain, the change in energy
DeltaEgap = agap(exx + eyy + ezz)
must be positive. This implies a negative value for agap.
[...] It is generally believed that the conduction band edge moves upward in
energy while the valence band moves downward, with most of the change being in
the conduction band egde, although Wei and Zunger recently argued that this is
not always the case."
Note also the comment of Wei and Zunger (Wei1):
"We show that the volume deformation potentials ac of the
conduction-band minimum state Gamma6c are usually large and always
negative (energy increases with pressure) while the volume deformation
potentials av of the VBM state Gamma8v are usually small
and negative for zinc blende compounds containing occupied valence d state
(e.g. GaAs, InAs) but positive for compounds without occupied valence d
orbitals (e.g. AlAs)."
Hydrostatic strain
-> 1Ddeformation_potentials_ReadInStrainTensor_hydro_nn3.in / nnp*.in
-> 1Ddeformation_potentials_hydro.in
- Now we want to apply a hydrostatic strain to our 1D structure (
strain-calculation =
hydrostatic-strain). The difference to
pseudomorphic strain is simply that the pressure acts equally from each
direction. This leads per definition to:
exx = eyy = ezz
for cubic crystals.
ezz is calculated in the
following way: ezz = - 2 (c12/c11)
exx (only for [001] growth direction!)
hydrostatic-strain
we artificially use inside the code the constant c12 = -c11/2
leading to ezz=exx.
This allows us to study the effects of absolute deformation potentials
only (without splitting of the bands and without shifts due to uniaxial
deformation potentials).
In this case we have:
exx = eyy = ezz = 0.07165
ehydro = Tr(eij) = exx + eyy + ezz
= 3exx = 0.21495
Ev' = Ev0 + av ehydro =
Ev0 + (-1.21*0.21495) = Ev0
- 0.26009
Ev(hh) = Ev0(hh) + av ehydro
= 0 - 0.26009 =
-0.260
Ev(lh) = Ev0(lh) + av ehydro
= 0 - 0.26009 =
-0.260
Ev(so) = Ev0(so) + av ehydro
= -0.341 - 0.26009 = -0.601
Ec'(Gamma) = Ec0(Gamma) + ac(Gamma)
ehydro = Ec0(G) + (-9.36
ehydro) = 1.519 - 2.0119 =
-0.492
Ec'(L) = Ec0(L)
+ ac(L) ehydro = Ec0(L)
+ (-4.91 ehydro) =
1.815 - 1.0554 = 0.759
Ec'(X) = Ec0(X)
+ ac(X) ehydro = Ec0(X)
+ (-0.16 ehydro) =
1.981 - 0.0343 = 1.946
Here we have negative hydrostatic pressure = increase in volume = positive
hydrostatic strain.
The valence bands shift downwards (av is negative) and
the conduction bands shift downwards, too (ac is
negative).
In this case, the Gamma conduction band is below the heavy/light hole band
edge.
Importing a strain tensor from a file It is also possible to
import a strain tensor from a file.
Here, we read in the file: StrainTensor_hydrostatic.dat
In this example, we apply no strain to InAs and a hydrostatic
strain to GaAs.
exx = eyy = ezz = 0.07165
ehydro = Tr(eij) = exx + eyy + ezz
= 3exx = 0.21495
position[nm] eps_xx
eps_yy
eps_zz
eps_xy eps_xz
eps_yz
9.500000000E+000 0.000000000E+000 0.000000000E+000
0.000000000E+000 0.000000000E+000 0.000000000E+000 0.000000000E+000 ! InAs
10.500000000E+000 71.649051431E-003 71.649051431E-003 71.649051431E-003
0.000000000E+000 0.000000000E+000 0.000000000E+000 ! GaAs
$simulation-flow-control
flow-scheme =
0
! Here, we use flow-scheme = 0
as we only calculate the strain.
strain-calculation = import-strain-simulation-coordinate-system
!
$end_simulation-flow-control
$import-data-on-material-grid
source-directory = "D:\My Strain Tensor
folder\"
filename-strain = StrainTensor_hydrostatic.dat
$end_import-data-on-material-grid
|