nextnano3 - Tutorial
next generation 3D nano device simulator
3D Tutorial
Intermediate-band solar cell (artificial quantum dot crystal)
Author:
Stefan Birner
If you want to obtain the input files that are used within this tutorial, please
check if you can find them in the installation directory.
If you cannot find them, please submit a
Support Ticket.
-> 3D_IBSolarCell_APL2007.in
Intermediate-band solar cell (artificial quantum dot crystal)
-> 3D_IBSolarCell_APL2007.in
This tutorial is based on the following paper:
[ShaoBalandin]
Intermediate-band solar cells based on quantum dot supracrystals
Q. Shao, A.A. Balandin, A.I. Fedoseyev, M. Turowski
Applied Physics Letters 91, 163503 (2007)
==> Fig. 2(a)
We calculate the superlattice energy dispersion for an artificial crystal
consisting of simple cubic QDs.
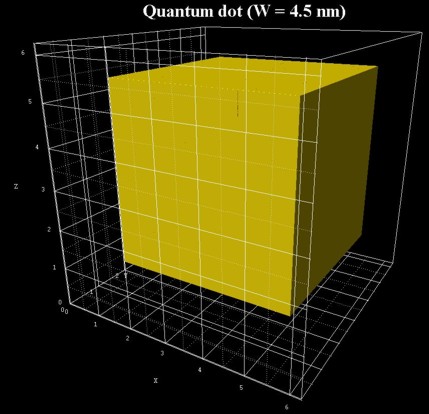
- The QD has a cubic shape with Wx = Wy = Wz
= 4.5 nm.
- The QDs are separated by a distance of Hx = Hy = Hz
= 2.0 nm.
- superlattice period: dx = dy = dz = 6.5
nm (di = Wi + Hi)
- We only model one QD and assume periodic boundary conditions along the
x, y and z direction.
- We solve the single-band Schrödinger equation for the Gamma conduction band only.
- The conduction band offset is assumed to be CBO = 1.290 eV,
i.e. the conduction band edge of the QD is at 0 eV, the
conduction band edge
of the barrier is at 1.290 eV.
- QD material: "InAs0.9N0.1",
barrier material: "GaAs0.98Sb0.02"
- effective electron masses:
QD: 0.0354 m0 ("InAs0.9N0.1"), barrier: 0.066 m0 ("GaAs0.98Sb0.02")
- grid spacing: 0.25 nm in x, y and z direction, i.e. 26 grid points in
each direction.
size of Schrödinger matrix to be solved: 26 * 26 * 26 = 17576
(10 eigenvalues are calculated)
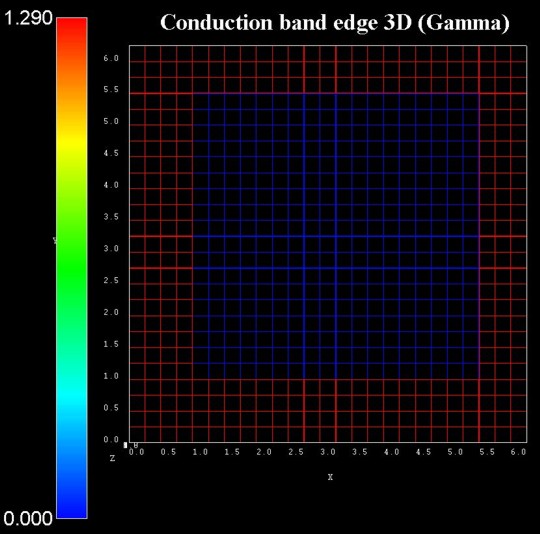
The following figure shows a 2D slice through the middle of the conduction
band edge highlighting the grid lines.
Required superlattice options
$numeric-control
...
!superlattice-option = 100-only ! for
dispersion along [100] direction in superlattice Brillouin zone, i.e. from Gamma
to X
superlattice-option = 110-only !
!superlattice-option = 111-only !
$quantum-model-electrons
...
model-name
= effective-mass !
number-of-eigenvalues-per-band = 10
! how many eigenenergies have to be calculated in each band
boundary-condition-100 =
periodic !
boundary-condition-010 =
periodic !
boundary-condition-001 =
periodic !
!num-ks-100
= 1
!
num-ks-100
= 11
!
!num-ks-010
= 1
!
num-ks-010
= 11
!
!num-ks-001
= 1
!
num-ks-001
= 11
!
Dispersion relation along [100] direction
superlattice-option = 100-only !
for dispersion along [100] direction in superlattice Brillouin zone, i.e.
from Gamma to X
The following figure shows the calculated dispersion relation along the [100]
direction.
The figure agrees qualitatively with Fig. 2(a) of the paper by [ShaoBalandin].
For the higher lying states inside the QD and above the QD, our results differ
quantitatively because we use the correct 3D QD confinement potential whereas [ShaoBalandin]
approximated the potential landscape with an analytical ansatz that
allows for the separation of the x, y and z variables. (This ansatz is only
justified for states confined deep inside the QD, i.e. in an energy region where the confinement inside the QD is
very strong.)
The energy levels of the single, uncoupled QD are close to the ones at q100
= 0 nm-1,
i.e. there is one confined state in the dot (corresponds to label 111).
All other states of the uncoupled dot are not confined.
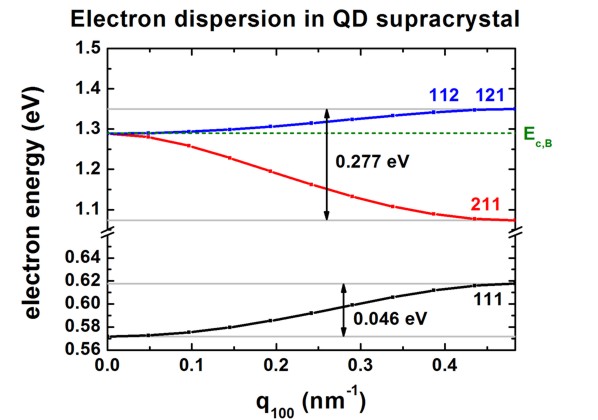
Ec,B is the
conduction band edge
energy of the barrier. The energy of the QD potential well is set
to 0 eV.
In the figure, the eigenstates are labeled with the quantum numbers nxnynz,
e.g. 111, 211, 112,
121.
112 and 121
are degenerate due to the symmetry of the structure.
(The superlattice vector "KSL" is often denoted as "q".)
The 111 miniband has a width of 0.046 eV, the next miniband has a width
of 0.277 eV.
These two minibands are separated by E23 = 0.455 eV where E23
is defined analogously to Fig. 2(b) of [ShaoBalandin].
The miniband formation is due to the strong electron wave function overlap.
Output
The output that was plotted in the above figure "Electron dispersion in QD
supracrystal " can be found in this file:
Schroedinger_1band/sg_dispSL3D_el_qc001_sg001_deg001_evmin001_evmax010.dat
This file contains information about the superlattice vector KSL
(in units of [pi/Li] and [1/Angstrom]), and the corresponding
eigenvalues.
norm[pi/L] norm[1/AA] k_x[pi/L_x] k_x[1/AA] k_y[pi/L_y] k_y[1/AA]
k_z[pi/L_z] k_z[1/AA] 1 2 3 ... 10
... ...
... ...
... ...
... ...
. . . ... .
See also this tutorial for one-dimensional superlattices:
Dispersion in infinite superlattices: Minibands
and this one for three-dimensional superlattice:
Artificial quantum dot crystal - Superlattice dispersion (minibands)
|