|
| |
nextnano3 - Tutorial
next generation 3D nano device simulator
2D Tutorial
Energy dispersion of a cylindrically shaped GaN nanowire
Author:
Stefan Birner
If you want to obtain the input files that are used within this tutorial, please
check if you can find them in the installation directory.
If you cannot find them, please submit a
Support Ticket.
-> 2DGaN_nanowire_nn3.in / *_nnp.in - input file for the nextnano3
and nextnano++ software
Energy dispersion of a cylindrically shaped GaN nanowire
In this tutorial we study the electron and hole energy levels of a two-dimensional
freestanding GaN nanowire of cylindrical shape.
The tutorial is based on the following paper:
X.W. Zhang, J.B. Xia
Optical properties of GaN wurtzite quantum wires
J. Phys.: Condens. Matter 18, 3107 (2006)
- We assume a cylindrically shaped GaN nanowire
(wurtzite structure) that has a radius of 2 nm with infinite barriers so
that the wave functions are zero at the nanowire boundary. This assumption is
consistent to the above cited paper. The GaN nanowire is shown in
red in the following figure. The GaN
nanowire is discretized on a mesh with a grid resolution of 0.05 nm.
Electrons
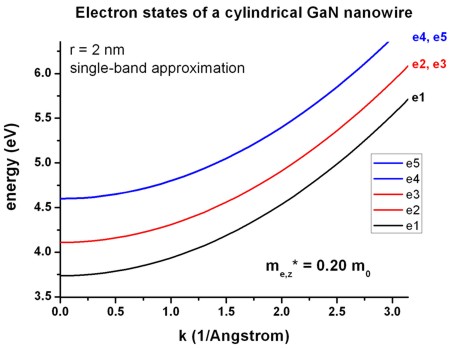
- The following figure shows the electron states as a function of k of the
GaN nanowire. It is in excellent agreement with Fig. 1 of the above cited
paper. All states are two-fold degenerate due to spin. In addition, the 2nd
and 3rd state are degenerate, as well as the 4th and
the 5th.
The ground state has quantum number L = 0. For L /= 0, the states are
degenerate due to L = +/- 1.
The energy levels increase with increasing k as quadratic terms of k
(parabolic dispersion).
Technical details: We calculated the electron energy levels at kz
= 0 with nextnano³ numerically by solving the 2D single-band
Schrödinger equation.
The parabolic dispersion for kz /= 0 has been calculated
analytically using Ei(kz)=Ei + hbar2
kz2 / (2m*), i.e. not with nextnano³.
The eigenvalues for kz = 0 can be found in the following file:
Schroedinger_1band/ev_cb1_sg1_deg1.dat
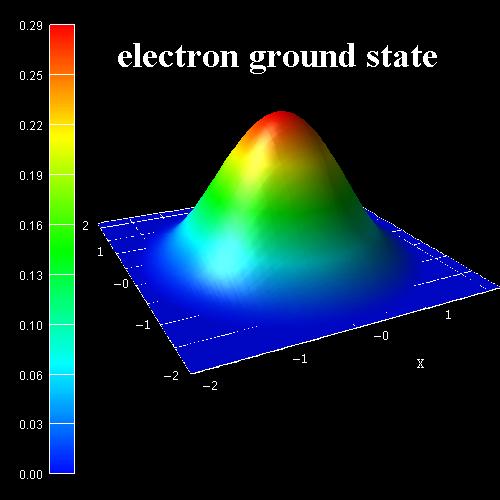
- The wave function (psi²) of the electron ground state at k = 0 is shown
in this figure.
Holes
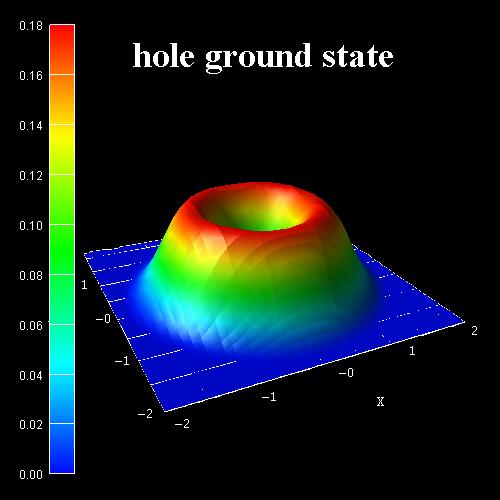
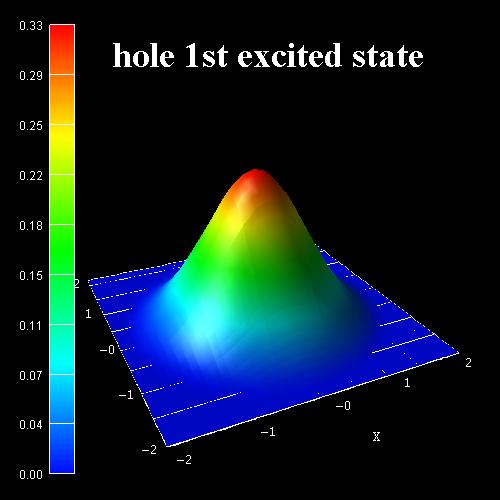
- The following figures show the ground state wave function (psi²) of the
hole (left figure) and the 1st excited hole state (right figure)
as calculated within the 6-band k.p approximation at k = 0.
According to the above cited paper, the right figure would be the ground
state for GaN nanowires with a radius < 0.7 nm. Because our nanowire has a
radius of 2 nm, the ground state wave function is according to the left
figure.
Following the paper of Zhang and Xia, this means that the probability for
electron-hole transitions (e1-h1) is not very high at a radius of 2 nm
because the wave functions don't have much overlap and the electron ground
state has L = 0, whereas the hole ground state has L = +/- 1
(dark exciton effect).
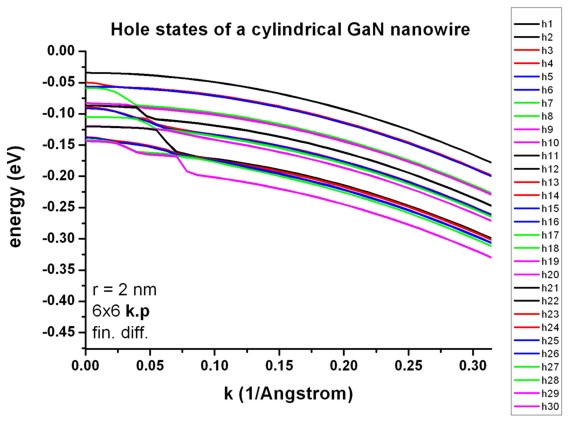
- The following figure shows the hole states as a function of k of the GaN
nanowire as calculated with 6-band k.p theory. It corresponds to Fig. 2
and Fig. 3 of the paper of Zhang and Xia. Note that the authors assumed the
hole energies to be positive.
All states are two-fold degenerate, i.e. h1=h2, h3=h4, h5=h6, ...
The nextnano³ results are a bit different. Several reasons could
explain this:
- The authors use the "cylindrical approximation" for the
k.p parameters. However, the parameters that they are citing are not
exactly cylindrical. Thus for our calculations, we had to employ the
parameters that they were citing (without making use of the cylindrical
approximation).
- Our cylinder does not have exactly cylindrical symmetry. It
is approximated to be cylindrical by a rectangular grid with a grid
resolution of 0.05 nm.
- For the k.p parameters that are given in the paper it
must hold:
A5 = 1/2 (L1 - M1)
A5 = 1/2 N1
0.0064.
The data that has been plotted in this figure is contained in this file:
Schroedinger_kp/kpar2D_disp_0_1_hl_6x6kp_ev_min001_ev_max030.dat
In the input file, one can specify the number of k|| = kz
points.
$quantum-model-holes
...
num-kp-parallel = 41
Note: 41 points means 16 minutes CPU
time (Intel i5, 2015). If one uses only 1, then one
only calculates the k.p states at kz=0 and the calculation takes
less than a minute.
- Zhang and Xia used the following 6-band k.p parameters:
Crystal field and spin-orbit splitting energies:
Deltacr = 0.021 Deltaso = 0.018
"Dresselhaus" parameters:
Zhang/Xia
nextnano³
========== =============
L = 6.3055 <==> L1 = -6.3055 - 1
= -7.3055 (!) ==> The definition of the
k.p Hamiltonians differs.
M = 0.1956 <==> M1 = -0.1956 - 1
= -1.1956 (!) ==>
N = 0.3813 <==> M2 = -0.3813 - 1
= -1.3813 (!) ==>
R = 6.1227 <==> N1 = -6.1227
S = 0.4335 <==> M3 = -0.4335 - 1
= -1.4335 (!) ==>
T = 7.3308 <==> L2 = -7.3308 - 1
= -8.3308 (!) ==>
Q = 4.0200 <==> N2 = -4.0200
Conversion to "Luttinger" parameters:
A1 = L2 + 1 = -8.3308
+ 1 = -7.3308
(!) ==> The definition of the k.p Hamiltonians differs.
A2 = M3 + 1 = -1.4335
+ 1 = -0.4335
(!) ==>
A3 = M2 - L2 = -0.3813 + 7.3308 = 6.9495
A4 = 1/2 (L1 + M1 - 2M3) =
-2.81705
A5 = 1/2 (L1 - M1)
= -3.05495 (!)
==> -3.06135
= 1/2 N1
= -3.06135 (!)
==> inconsistent to -3.05495
A6 = SQRT(2)/2 N2
= -2.84256926
- cylindrical (axial) approximation
L
- M - R
= 0
L1
- M1 - N1
= 0
==> (A2+A4+A5-1) - (A2+A4-A5-1) - 2A5 = 0
A1 - A2 = -A3 = 2 A4
A3 + 4 A5 =
SQRT(2) A6
Delta2 = Delta3 = 1/3 Deltaso
|