|
| |
nextnano3 - Tutorial
next generation 3D nano device simulator
1D Tutorial
k.p dispersion in bulk unstrained, compressively and tensilely strained GaN (wurtzite)
Author:
Stefan Birner
If you want to obtain the input files that are used within this tutorial, please
check if you can find them in the installation directory.
If you cannot find them, please submit a
Support Ticket.
-> bulk_kp_dispersion_GaN_unstrained_0_nn3.in
/ *_nnp.in - input file for nextnano3
/ nextnano++ software
-> bulk_kp_dispersion_GaN_unstrained_90_nn3.in
/ *_nnp.in -
-> bulk_kp_dispersion_GaN_strain_compressive_0_nn3.in / *_nnp.in
-
-> bulk_kp_dispersion_GaN_strain_compressive_90_nn3.in / *_nnp.in -
-> bulk_kp_dispersion_GaN_strained_tensile_0_nn3.in /
*_nnp.in -
-> bulk_kp_dispersion_GaN_strained_tensile_90_nn3.in /
*_nnp.in -
-> bulk_kp_dispersion_GaN_strained_tensile_90_3D_nn3.in / *_nnp.in -
This tutorial is based on
[ParkChuangPRB1999]
Crystal-orientation effects on the piezoelectric field and electronic
properties of strained wurtzite semiconductors
S.-H. Park, S.-L. Chuang
Phys. Rev. B 59, 4725 (1999).
Further material parameters used in the calculations are taken from
[KumagaiChuangAndoPRB1998]
Analytical solutions of the block-diagonalized Hamiltonian for strained
wurtzite semiconductors
M. Kumagai, S. L. Chuang, H. Ando
Phys. Rev. B 57, 15303 (1998).
We calculate E(k) for bulk GaN (unstrained), with compressive and with
tensile strain, along two different growth directions.
k.p dispersion in bulk unstrained GaN (wurtzite)
- We want to calculate the dispersion E(k) from |k|=0 to |k|=1.0
[1/nm] along the
following directions in k space:
- [100] to [001]
- [110] to [001]
- [111] to [001]
We compare 6-band k.p theory results vs. single-band (effective-mass)
results for unstrained GaN.
Calculating the bulk k.p dispersion
$output-kp-data
destination-directory = kp/
bulk-kp-dispersion = yes
! calculate bulk k.p dispersion
grid-position = 2.0 ! [nm]
!----------------------------------------
! Dispersion along [100] direction
! maximum |k| vector = 1.2 [1/nm]
!----------------------------------------
k-direction-to-k-point = 1.2 0.0 0.0 ! [1/nm]
!
related to output file kp_bulk/bulk_6x6kp_dispersion_as_in_inputfile_kxkykz_000_kxkykz.dat
number-of-k-points = 100 !
number of k points to be calculated (resolution)
The maximum value
of |k| is 1.2 [1/nm].
Note that for values of |k| larger than
1.0 [1/nm],
k.p theory might not
be a good
approximation any more.- We calculate the pure bulk dispersion at
grid-position = 2.0,
i.e. for the material located at the grid point at 2 nm.
In our case this is
GaN but it could be any strained alloy. If strain is present (see below), the k.p
Bir-Pikus strain Hamiltonian will be diagonalized at each k point.
The grid point at grid-position must be located inside a quantum cluster.
shift-holes-to-zero = yes forces the
top of the valence band to be located at 0 eV.
In this tutorial, however, we use no.
Out zero point of energy is the "average" energy of all three hole bands.
Here, "average" means without taking crystal field and spin-orbit splitting
into account. This is added afterwards to get the energies of heavy hole
(HH), light hole (LH) and crystal-field split-off hole (CH).
How often the bulk k.p Hamiltonian should be solved can be specified
via number-of-k-points. To increase the resolution, just increase
this number.
- The results can be found in:
kp_bulk/bulk_6x6kp_dispersion_as_in_inputfile_kxkykz_000_kxkykz.dat - along the path from [100] to
[000] (Gamma point) and to [001]
kp_bulk/bulk_sg_dispersion.dat
- along the path from [100] to [000]
(Gamma point) and to [001]
kp/bulk_sg_dispersion.dat (single-band approximation)
- along the path from [100] to [000]
(Gamma point) and to [001]
The following figure shows the bulk k.p dispersion of unstrained GaN
(wurtzite).
The kz direction corresponds to the c axis [0001].
The dispersion along kx and ky is identical (only kx
is shown), i.e. the dispersion in the (001) plane is isotropic.
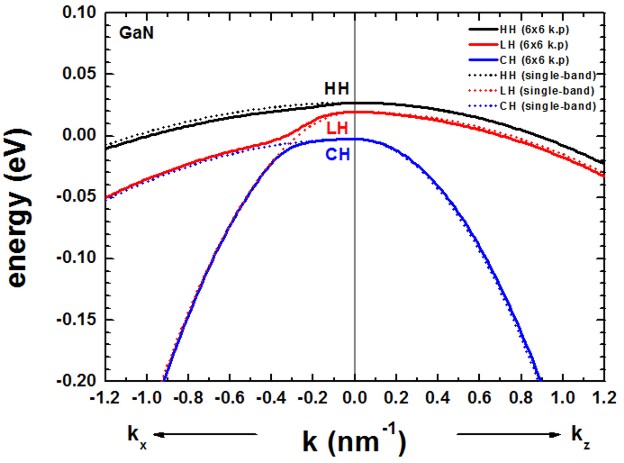
The results of our figure is in excellent agreement to Fig. 4 (b) of the paper
[KumagaiChuangAndoPRB1998].
- The dispersion along the hexagonal c axis is substantially different.
If the average of the three valence band edges (without taking
crystal-field and spin-orbit splitting into account) is defined to be at zero,
i.e. Ev,av = 0 eV, then the energies E1,
E2 and
E3 are defined as follows for the
unstrained case:
E1 = Delta1 + Delta2
E2 = B + A
E3 = B
- A
where Delta1 is the crystal field split energy Deltacr,
and Delta2 and Delta3 are related to the spin-orbit
split off-energy Deltaso as follows:
Delta2 = Delta3 = 1/3 Deltaso
B = (Delta1
- Delta2)/ 2.
A = SQRT(B2 + 2 Delta32)
The Delta parameters are defined in the database
6x6-kp-parameters = ...
0.0220 0.005 0.005 ! Delta1(cr),Delta2=Delta_so/3,Delta3=Delta_so/3
leading to:
B = 0.0085
A = 0.01106
E1 = Delta1 + Delta2 = 0.027 eV
E2 = B + A = 0.0085 +
0.01106 = 0.01956
eV
E3 = B - A =
0.0085
-
0.01106 =
-0.00256 eV
- In contrast to zinc blende materials, even in the unstrained case, the
heavy and light hole are not degenerate at k = 0.
- For comparison, we also show the dispersion using the single-band
effective mass approximation (dotted lines).
We used the following values for the effective hole masses, according to
reference
http://www.ioffe.rssi.ru/SVA/NSM/Semicond/GaN/bandstr.html.
mHH,a = 1.6 [m0], mHH,c = 1.1
[m0]
mLH,a = 0.15 [m0], mLH,c
= 1.1 [m0]
mCH,a = 1.1 [m0],
mCH,c = 0.15 [m0]
valence-band-masses =
1.6 1.6 1.1 ! HH m_|_, m_|_,
m|| (with respect to c-axis)
0.15 0.15 1.1 !
LH m_|_, m_|_, m||
(with respect to c-axis)
1.1 1.1 0.10 !
CH m_|_, m_|_, m||
(with respect to c-axis)
- The effective mass approximation is a simple parabolic dispersion which is
isotropic in zinc blende materials (i.e. no dependence on the k
vector direction) but is anisotropic for wurtzite materials due to the
different effective masses paralllel and perpendicular to the c axis.
k.p dispersion in compressively and tensilely strained GaN (wurtzite)
- We compare two different orientations of the crystal coordiate system with
respect to the simulation coordinate system.
Case a) Default orientation: hexagonal c axis oriented along the z
direction [0001]
Case b) Rotation of hexagonal c axis by 90 degrees so that it oriented
along the default x direction [10-10]
The orientation of the y axis remains the same.
$domain-coordinates
...
growth-coordinate-axis = 0 0 1 !
along z direction of simulation coordinate system
!-----------------------------------------------------------------------------------------
! The angle theta is defined as the angle between the growth direction z'
and the c axis.
! Angle theta = 0░ corresponds to the z' = [0001] growth direction.
!-----------------------------------------------------------------------------------------
hkil-x-direction = 1 0 -1 0 ! Miller
Indices of x-coordinate axes direction (DEFAULT)
!hkil-y-direction = -1 2 -1 0 ! Miller
Indices of y-coordinate axes direction (DEFAULT)
hkil-z-direction = 0 0 0 1 !
Miller Indices of z-coordinate axes direction (DEFAULT)
!-----------------------------------------------------------------------------------------
!-----------------------------------------------------------------------------------------
! Angle theta = 90░ corresponds to the z' = [10-10] growth direction.
!-----------------------------------------------------------------------------------------
hkil-x-direction = 0 0 0 -1 !
Miller Indices of x-coordinate axes direction
!hkil-y-direction = -1 2 -1 0 ! Miller
Indices of y-coordinate axes direction
hkil-z-direction = 1 0 -1 0 !
Miller Indices of z-coordinate axes direction
!-----------------------------------------------------------------------------------------
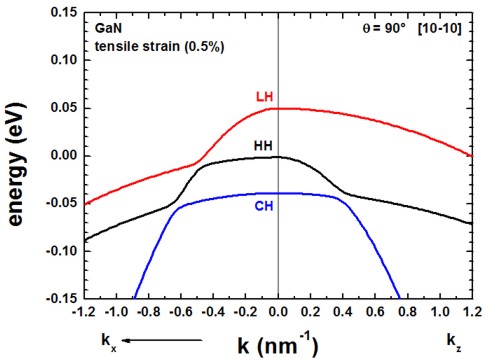
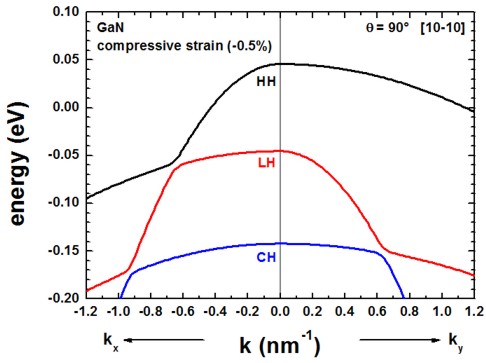
The following figures compare the 6-band k.p valence band dispersion relation of
compressively (-0.5%, figure on the left) vs. tensilely (+0.5%, figure on
the right) strained GaN.
Assuming that the substrate material is Al(x)In(1-x)N,
- a compressive strain of -0.5% corresponds to Al0.785In0.215N
(exx = eyy = -0.005)
- a tensile strain of 0.5% corresponds to Al0.859In0.141N
(exx = eyy = 0.005)
using the lattice constants given in the references cited above.
The results for tensile strain indicate that the light hole (LH)
band is higher in energy than the heavy hole (HH) band.
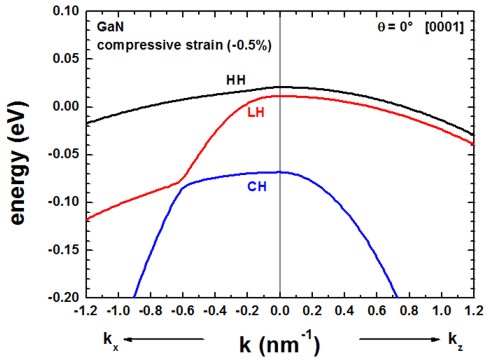 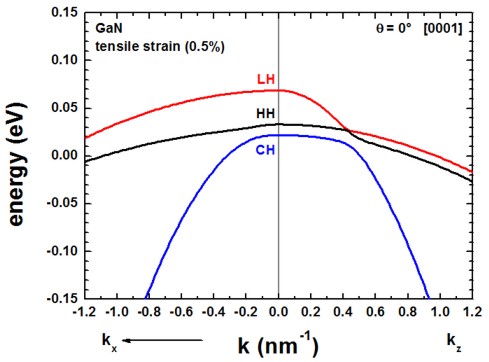
The results of these two figures can be found in this file:
kp/bulk_6x6kp_dispersion_100_000_001.dat
where 100 represents the kx direction, 000
the Gamma point and 001 the kz direction, i.e.
the plotted dispersion is a cut through the 3D Brillouin zone along these lines.
We only plotted the result for kx. The dispersion along ky
is identical in this case. Also the dispersion along [110], i.e. the dispersion
is isotropic with respect to the (001) plane.
Once the c axis is oriented along the z axis of the simulation coordinate system
(rotation by 90 degrees around the y axis, c axis along [10-10] direction),
the corresponding results look as follows.
Actually the .log file (screen output) of the simulation indicates
the rotation angle and the rotation axis:
==> rotation angle = 90.000000000 ░ = 0.500000000 [pi] =
1.570796327
==> rotation axis = [ 0.000000000 1.000000000 0.000000000 ]
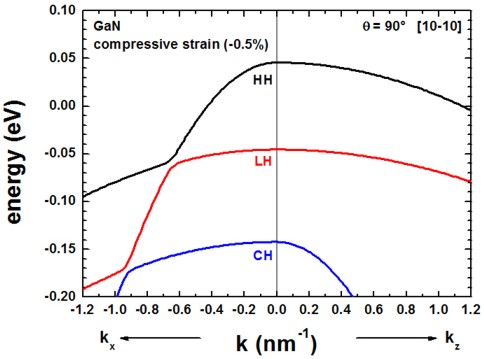 
 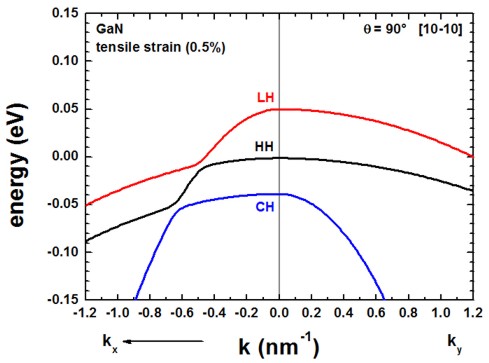
The results of these two figures can be found in this file:
kp/bulk_6x6kp_dispersion_100_000_001.dat
where 100 represents the kx direction, 000
the Gamma point and 001 the kz direction, i.e.
the plotted dispersion is a cut through the 3D Brillouin zone along these lines.
The results for the dispersion along ky is now different from the
dispersion along kx.
The results for ky are contained in this file
kp/bulk_6x6kp_dispersion_000_kxkykz.dat
because here we specified in the input file to calculate the dispersion
from the Gamma point (0,0,0) to (kx,ky,kz) = (0
, 1.2 nm-1 , 0).
$output-kp-data
k-direction-to-k-point = 0.0 1.2 0.0 !
(kx,ky,kz) in units of [1/nm]
Note: For theta = 90░, we have rotated the crystal (cr) coordinate system with
respect to the simulation (sim) coordinate system.
Therfore, for our new orientation it holds eyy,cr = eyy,sim
= +-0.005 and exx /= eyy.
The results of our figures are in excellent agreement to figures 5 and 6 of the paper
[ParkChuangPRB1999].
Note that for the case of tensile strain and orientation of the c axis along the
[10-10] orientation, the strain tensor component along the y direction of the
simulation system is tensilely strained whereas the component along the x
direction is compressively (!) strained.
For a discussion of the figures please refer to the paper of Park and Chuang.
Energy dispersion E(k) in three dimensions
Alternatively one can print out the 3D data field of the bulk E(k) =
E(kx,ky,kz) dispersion.
$output-kp-data
...
bulk-kp-dispersion-3D =
yes
grid-position = 2.0
! in units of [nm]
!----------------------------------------
! maximum |k| vector = 1.2 [1/nm]
!----------------------------------------
k-direction-to-k-point
= 1.2 0.0 0.0 ! k-direction
and range for dispersion plot [1/nm]
number-of-k-points = 20
! number of k points to calculated (resolution)
The meaning of number-of-k-points =
20 is the following:
20 k points from '- maximum |k| vector'
to zero
(plus the Gamma point) and
20 k points from zero to '+ maximum |k| vector'
(plus the Gamma point) along all three directions,
i.e. the whole 3D volume then contains
21 * 21 * 21 = 9261 k points.
Left: A 2D slice in the (kx,ky) plane for kz=0
of the highest lying hole state for the tensilely strained GaN (oriented along
90 degrees, i.e. z is oriented along [10-10]) is shown in this figure.
Right: Horizontal and vertical slice through the center coordinate at (kx,ky,kz)
= (0,0,0).
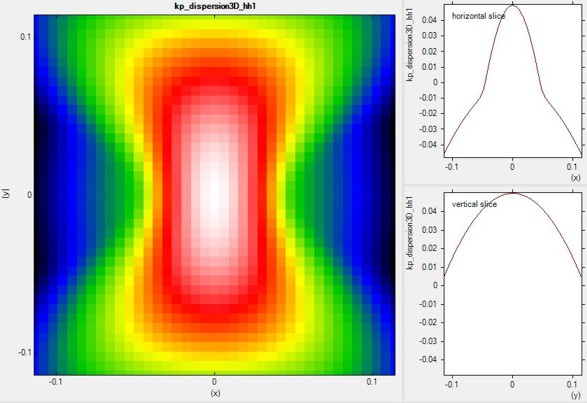
|